(x2 +4) . (x2-4)=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) x = -1. b) x = 4 hoặc x = 5.
c) x = ± 2 . d) x = 1 hoặc x = 2.

a: \(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)
b: \(\Leftrightarrow x\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)

Đáp án: D
(x2 - 4) (x2 - 1) = 0 ⇔ x = ±2; x = ±1 nên A = {-2; -1; 1; 2}
(x2 - 4) (x2 + 1) = 0 ⇔ x2 - 4 = 0 ⇔ x = ±2 nên B = {-2; 2}
x4 - 5x2 + 4)/x = 0 ⇔ x4 - 5x2 + 4 = 0 ⇔ x = ±2; x = ±1 nên D = {-2; -1; 1; 2}
=> A = D

1.
\(x^2-5x+6=0\\ \Rightarrow x^2-2x-3x+6=0\\ \Rightarrow\left(x^2-2x\right)-\left(3x-6\right)=0\\ \Rightarrow x\left(x-2\right)-3\left(x-2\right)=0\\ \Rightarrow\left(x-2\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=3\end{matrix}\right.\)
2.
\(\left(x+4\right)^2-\left(3x-1\right)^2=0\\ \Rightarrow\left(x+4-3x+1\right)\left(x+4+3x-1\right)=0\\ \Rightarrow\left(-2x+5\right)\left(4x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}-2x+5=0\\4x+3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\x=-\dfrac{3}{4}\end{matrix}\right.\)
3.
\(x^2-2x+24=0\\ \Rightarrow\left(x^2-2x+1\right)+23=0\\ \Rightarrow\left(x-1\right)^2+23=0\)
Vì (x-1)2≥0
23>0
\(\Rightarrow\left(x-1\right)^2+23>0\)
Vậy x vô nghiệm
4.
\(9x^2-4=0\\ \Rightarrow\left(3x-4\right)\left(3x+4\right)=0\\ \Rightarrow\left[{}\begin{matrix}3x-4=0\\3x+4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-\dfrac{4}{3}\end{matrix}\right.\)
5.
\(x^2+2x-8=0\\ \Rightarrow\left(x^2+2x+1\right)-9=0\\ \Rightarrow\left(x+1\right)^2-3^2=0\\ \Rightarrow\left(x-2\right)\left(x+4\right)=0\\ \Rightarrow\left[{}\begin{matrix}x-2=0\\x+4=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\)

\(\left(x+3\right)\left(1-x\right)>0.\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3>0.\\1-x>0.\end{matrix}\right.\\\left\{{}\begin{matrix}x+3< 0.\\1-x< 0.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x>-3.\\x< 1.\end{matrix}\right.\\\left\{{}\begin{matrix}x< -3.\\x>1.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow-3< x< 1.\)
\(\left(x^2-1\right)\left(x^2-4\right)< 0.\\ \Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2-1< 0.\\x^2-4>0.\end{matrix}\right.\\\left\{{}\begin{matrix}x^2-1>0.\\x^2-4< 0.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2< 1.\\x^2>4.\end{matrix}\right.\\\left\{{}\begin{matrix}x^2>1.\\x^2< 4.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\left[{}\begin{matrix}x< 1.\\x>-1.\end{matrix}\right.\\\left[{}\begin{matrix}x>2.\\x< -2.\end{matrix}\right.\end{matrix}\right.\\\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1.\\x< -1.\end{matrix}\right.\\\left[{}\begin{matrix}x< 2.\\x>-2.\end{matrix}\right.\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}-1< x< 1.\\\left[{}\begin{matrix}x>2.\\x< -2.\end{matrix}\right.\end{matrix}\right.\\\left\{{}\begin{matrix}\left[{}\begin{matrix}x>1.\\x< -1.\end{matrix}\right.\\-2< x< 2.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x>2.\\x< -2.\\-2< x< -1.\\1< x< 2.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x< -2.\\x>2.\end{matrix}\right.\)

\(\Leftrightarrow\left(x^4+5x^2+6\right)\left(x^4+5x^2+4\right)-24\)
Đặt \(x^4+5x^2+6=t\)
\(t\left(t-2\right)-24=t^2-2t-24\)
\(\Leftrightarrow t^2-2t+1-25=\left(t-1\right)^2-5^2=\left(t-6\right)\left(t+4\right)>0\)
TH1 : \(\left\{{}\begin{matrix}t-6>0\\t+4>0\end{matrix}\right.\Leftrightarrow t>6\)
TH2 : \(\left\{{}\begin{matrix}t-6< 0\\t+4< 0\end{matrix}\right.\)<=> t < -4
Theo cách đặt \(x^4+5x^2+6>6\Leftrightarrow x^2\left(x^2+5\right)>0\)* luôn đúng *
\(x^4+5x^2+6< -4\Leftrightarrow x^4+5x^2+10< 0\)
\(\Leftrightarrow x^4+\dfrac{2.5}{2}x^2+\dfrac{25}{4}+\dfrac{15}{4}< 0\Leftrightarrow\left(x^2+\dfrac{5}{2}\right)^2+\dfrac{15}{4}< 0\)( vô lí )
Cậu làm thiếu rất nhiều bước và có thể người khác sẽ khó hiểu. Xem cách trình bày của mình nè.

a, \(\Rightarrow x-2\inƯ\left(-3\right)=\left\{\pm1;\pm3\right\}\)
| x-2 | 1 | -1 | 3 | -3 |
| x | 3 | 1 | 5 | -1 |
b, \(3\left(x-2\right)+13⋮x-2\Rightarrow x-2\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
| x-2 | 1 | -1 | 13 | -13 |
| x | 3 | 1 | 15 | -11 |
c, \(x\left(x+7\right)+2⋮x+7\Rightarrow x+7\inƯ\left(2\right)=\left\{\pm1;\pm2\right\}\)
| x+7 | 1 | -1 | 2 | -2 |
| x | -6 | -8 | -5 | -9 |

Tọa độ giao điểm của 2đường tròn đã cho thỏa mãn hệ phương trình:
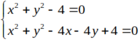 ⇔
⇔
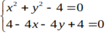
⇔
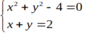 ⇔
⇔
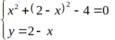
⇔
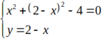 ⇔
⇔
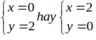
Vậy giao điểm A(0; 2) và B( 2;0).
Chọn C.
Ta có : ( x2 +4)(x2 - 4) = 0 (*)
Vì x2 + 4 > 0 , \(\forall x\) => (*) <=> \(x^2-4=0\Leftrightarrow\left(x-2\right)\left(x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
Vậy ........