Cho hình thang cân ABCD( AB//CD). Qua B kẻ đường thằng song song với AC cắt đường thẳng DC tại E. Chứng minh:
a) Tứ giác ABED là hình thang
b) Tam giác BDE là tam giác cân
c) Các tam giác ACD và BDC bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác AEMF có
AE//MF
ME//AF
Do đó: AEMF là hình bình hành
mà AE=AF
nên AEMF là hình thoi

a: Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi

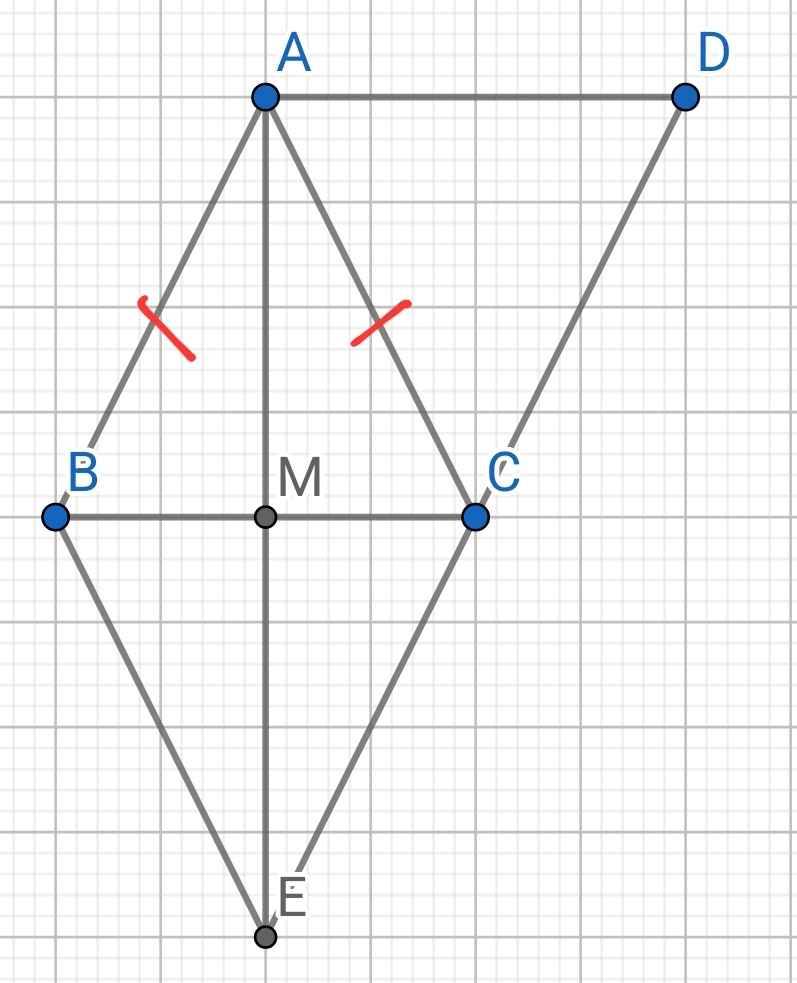
a: Xét tứ giác ABEC có
AB//EC
AC//BE
=>ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi
b: ABEC là hình thoi
=>AE vuông góc BC
 Do ABCD là hình bình hành (gt)
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AB // CE
Tứ giác ABEC có:
AB // CE (cmt)
BE // AC (gt)
⇒ ABEC là hình bình hành
Mà AB = AC (gt)
⇒ ABEC là hình thoi
b) Do ABCD là hình thoi (cmt)
AE và BC là hai đường chéo của hình thoi
⇒ AE ⊥ BC
a Xét tứ giác ABED có AB//ED
nên ABED là hình thang
b:
Xét tứ giác ABEC có
AB//EC
AC//BE
Do đó: ABEC là hình bình hành
Suy ra: AC=BE
Ta có: ABCD là hình thang cân
nên AC=BD
mà AC=BE
nên BD=BE
=>ΔBDE cân tại B
c: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC