dựa vào chĩnh vẽ hãy chứng minh a//b
a b M 55độ 35độ O N
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 5 2022
cửa hàng bán được một tạ rưỡi gẹo tẻ và gạo nếp ; trong đó 25% là gạo nếp. hỏi của hàng bán mỗi loại bao nhiêu ki-lô-gam gạo
CM
2 tháng 4 2017
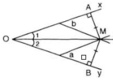
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.
24 tháng 5 2022
a: \(A=\left(\sin^210^0+\sin^280^0\right)+\left(\sin^220^0+\sin^270^0\right)+...+\left(\sin^240^0+\sin^250^0\right)\)
=1+1+1+1
=4
b: \(B=\left(\cos^215^0+\cos^275^0\right)+\left(\cos^225^0+\cos^265^0\right)+...+\cos^245^0\)
\(=1+1+1+1+\dfrac{1}{2}=\dfrac{9}{2}\)
28 tháng 4 2023
a: góc AMO+góc ANO=90+90=180 độ
=>AMON nội tiếp
b: Xet ΔAMB và ΔACM có
góc AMB=góc ACM
góc MAB chung
=>ΔAMB đồng dạng với ΔACM
=>AM^2=AB*AC=AM*AN
c: AB*AC=AM^2=AO^2-R^2
Sửa lại :
Trên tia đối của tia Ma lấy N ; trên tia đối của tia Nb lấy C.
Vẽ Ox // a (1). Ta có :
$\widehat{OMB}=\widehat{MOx}=55^o$ (so le trong)
Mà $\widehat{MOx}+\widehat{xON}=\widehat{MON}=90^o$
$=>55^o+\widehat{xON}=90^o$
$=>\widehat{xON}=35^o$
$=>\widehat{xON}=\widehat{ONC}=35^o$
Mà hai góc này nằm ở vị trí so le trong
=> Ox // b (2)
Từ (1)(2) => a // b.
Trên tia đối của tia Ma lấy B ; trên tia đối của tia Nb lấy C.
Vẽ Ox // a (1). Ta có :
$\widehat{OMB}=\widehat{MOx}=55^o$ (so le trong)
Mà $widehat{MOx}+\widehat{xOn}=\widehat{MON}=90^o$
$=>\55^o+\widehat{xOn}=90^o$
$=>\widehat{xOn}=35^o$
$=>\widehat{xOn}=\widehat{ONC}=35^o$
Mà hai góc này nằm ở vị trí so le trong
=> Ox // b (2)
Từ (1)(2) => a // b.