A chạy với vận tốc đều và B chạy nhanh gấp x lần A (x > 1). A đứng trước B y mét , sau đó 2 người bắt đầu chạy theo cùng 1 hướng. Hỏi B chạy bao nhiêu mét để bắt kịp A?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1, 1.2 giờ
2 9 giờ 30 phút - 8 = 1 giờ 30 phút = 1.5 giờ
. quãng đường xe máy đi lúc đầu là:
1.5*32 = 48 (km)
ta có phương trình
48 + 32x = 56x
=> x = 2
ô tô đuổi kịp xe máy vào thời gian là: 9 giờ 30 phút + 2 giờ = 11 giờ 30 phút
3.
5 phút = 0.08(3) giờ
quãng đường đi = 0.08(3) * 120 = 10(km)
Gọi quãng đường của mỗi chặng là S (km)
Quãng đường AB = 3S.
Thời gian đi chặng thứ nhất là: t1 = S/v1 = S/72
Thời gian đi chặng thứ hai là: t2 = S/v2 = S/60
Thời gian đi chặng thứ ba là t3 = S/v3 = S/40
Theo giả thiết: t1+t2+t3=4 <=> S/72 + S/60 + S/40 = 4
<=> S(1/72 + 1/60 + 1/40) = 4
<=> S.1/18 = 4
<=> S= 4.18 = 72 (km)
Vậy quãng đường AB là: 3.S = 3.72 = 216 (km)

| \(\sqrt{\sqrt[]{}\frac{ }{ }\hept{\begin{cases}\\\end{cases}}\hept{\begin{cases}\\\\\end{cases}}\orbr{\begin{cases}\\\end{cases}}^{ }^2_{ }}\) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
&nbs

11 tháng 7 2017
Theo đó, xét rằng vì khoảng cách giảm dần nên thời gian cần thiết để thực hiện di chuyển những khoảng cách đó cũng giảm dần. Vì thế mà tới một lúc nào đó, thời gian giảm đến 0 và Achiles sẽ bắt kịp chú rùa. |
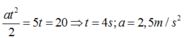
Gọi quãng đường A đến khi gặp nhau là a (m)
Quãng đường B đi đến chỗ gặp nhau là b(m)
Từ lúc bắt đầu đi đến khi gặp nhau, A và B đi cùng một khoảng thời gian
Mà quãng đường tỉ lệ thuận với vận tốc ; vận tốc của B gấp x lần vận tốc của A
=> Quãng đường B đi gấp x lần quãng đường A đi
=> b = x.a
Mặt khác, b = y + a => x.a = y + a => (x - 1)a = y => a = y/(x - 1)
Vậy B đi quãng đường dài b = x.y/ (x - 1) (m)