Cho tam giác ABC nhọn, BD và CE là hai đường cao. Các điểm M và N trên các đường cao BD và CE sao cho goca AMB = góc ANC = 90o. CM: tam giác AMN cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

10 tháng 5 2023
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB
ΔANB vuông tại N có NE vuông góc AB
nên AN^2=AE*AB
ΔAMC vuông tại M có MD vuông góc AC
nên AM^2=AD*AC
=>AN=AM

12 tháng 5 2023
1: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
2: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
3: ΔAMC vuông tại M có MD vuông góc AC
nên AD*AC=AM^2
ΔANB vuông tại N có NE vuông góc AB
nên AE*AB=AN^2
=>AM=AN
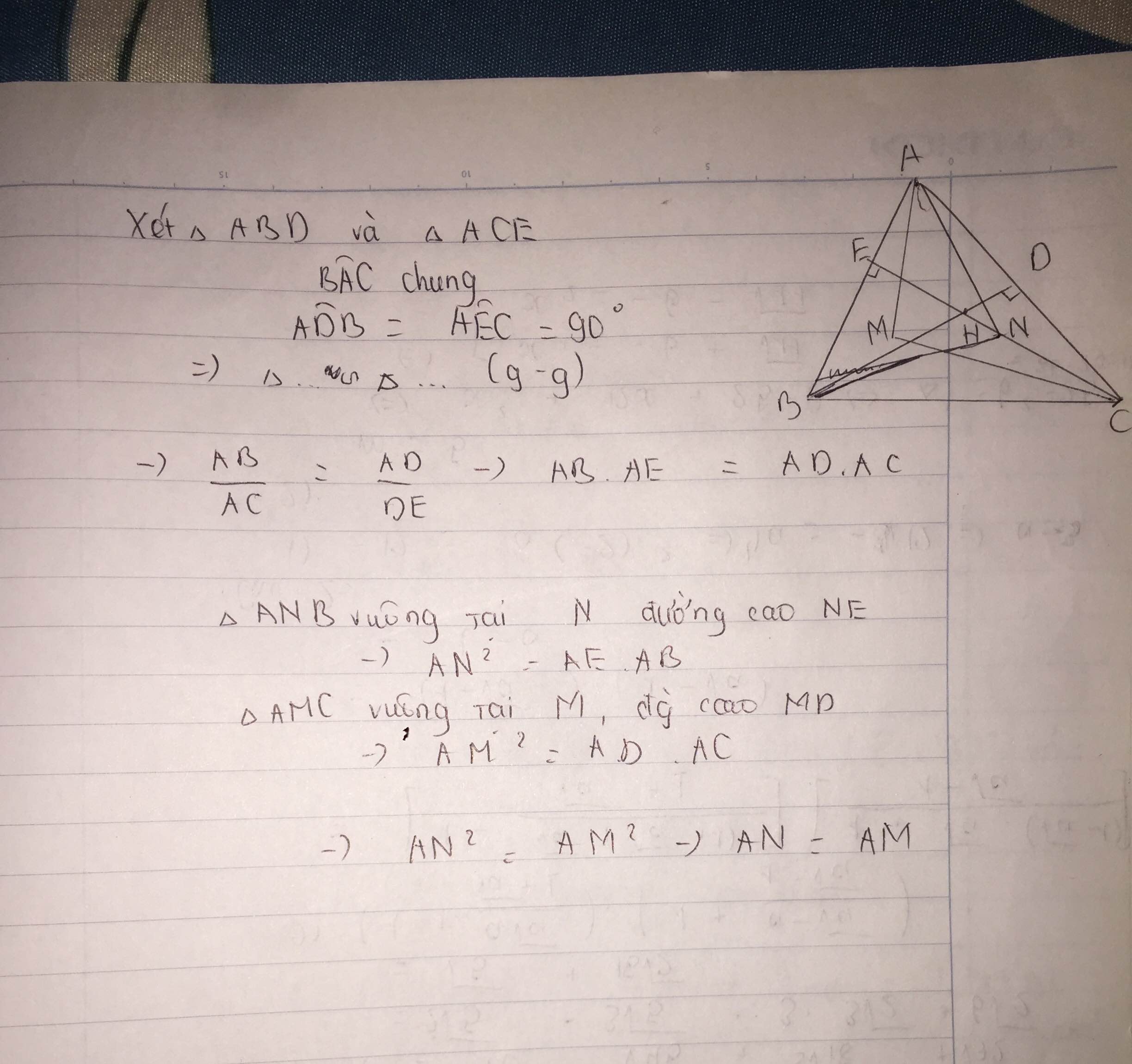
Xét ΔAMB vuông tại M có ME là đường cao
nên \(AE\cdot AB=AM^2\left(1\right)\)
Xét ΔANC vuông tại N có ND là đường cao
nên \(AN^2=AD\cdot AC\left(2\right)\)
Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc EAC chung
Do đó: ΔADB\(\sim\)ΔAEC
Suy ra: AD/AE=AB/AC
hay \(AD\cdot AC=AB\cdot AE\left(3\right)\)
Từ (1), (2) và (3) suy ra AM=AN
hay ΔAMN cân tại A