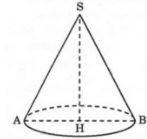
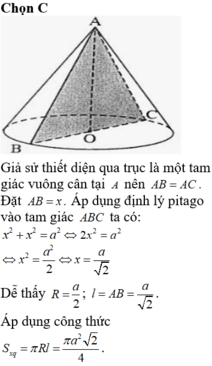
Cắt một hình nón bằng một mặt phẳng qua trục của nó ta được thiết diện là một tam giác đều cạnh a\(\sqrt{3}\) . Diện tích xung quanh của hình nón là
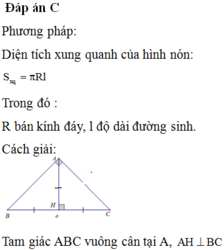
A. S\(_{xq}\)=\(\dfrac{3}{4}\)πa2 B. S\(_{xq}\)=\(\dfrac{3\sqrt{3}}{8}\)πa2 C. S\(_{xq}\)=\(\dfrac{3}{2}\)πa2 D. S\(_{xq}\)=\(\dfrac{3\sqrt{3}}{4}\) πa2



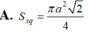
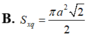



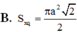
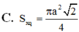
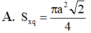

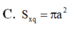



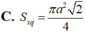
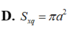
Lời giải:
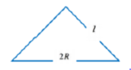
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C