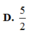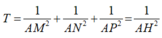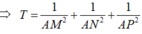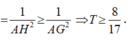Cho tứ diện đều SABC cạnh a. (P) là một mặt phẳng thay đổi đi qua đỉnh S và song song với BC. Giả sử (P) cắt các cạnh AB, AC lần lượt tại M và N
a) Cho biết tính chất của tam giác SMN
b) Chứng minh rằng mặt phẳng (P) luôn đi qua một đường thẳng cố đinh
c) Đặt AM = \(x\). Tính \(y=SM^2+SN^2+MN^2\). Tìm \(x\) để \(y=\dfrac{7a^2}{4}\) ?