Cho hình chóp S.ABCD có đáy ABCD là hình bình hành, cho điểm M thay đổi trên cạnh SD. Gọi I, J lần lượt là giao điểm của AN với BM và AM với BN. Chứng minh rằng khi M chạy trên cạnh SD thì I, J lần lượt chạy trên các đường thẳng cố định ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 6 2019
Trong mặt phẳng (ABCD) ta có AC cắt BD tại O, IJ cắt BD tại E.
Trong mặt phẳng (SBD), ME cắt SO tại G. ta có G thuộc (MIJ)
(MIJ) chứa IJ // AC nên giao tuyến của (MIJ) với (SAC) là đường thẳng qua G và song song với AC, đường thẳng này cắt SA tại N, cắt SC tại P.
Vậy thiết diện là ngũ giác MNIJ.
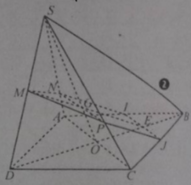
Đáp án D
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
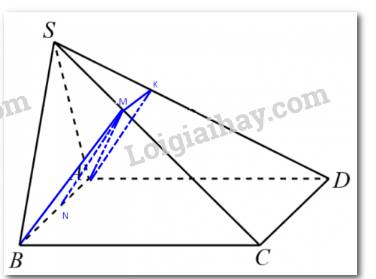
a) Ta có: \(\left( {ABM} \right) \cap \;\left( {ABCD} \right) = AB,\;\left( {ABCD} \right) \cap \;\left( {SCD} \right) = CD,\;AB//CD\).
Suy ra giao tuyến của (ABM) và (SCD) là đường thẳng qua M song song với AB và CD.
Qua M kẻ MK song song với CD (K thuộc SD).
Vậy, K là giao điểm của (AMN) và SD.
Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{SK}}{{SD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
b) Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{MK}}{{CD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
Lại có \(\frac{{AN}}{{AB}} = \frac{1}{3}\), AB=CD suy ra AN = MK.
Xét tứ giác ANMK ta có: AN = MK, AN // MK suy ra ANMK là hình bình hành.
Do đó MN // AK hay MN // (SAD).
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 12 2021
a.
Do O là tâm hbh \(\Rightarrow\) O là trung điểm AC
\(\Rightarrow OJ\) là đường trung bình tam giác SAC
\(\Rightarrow OJ||SA\)
Mà \(SA\in\left(SAC\right)\Rightarrow OJ||\left(SAC\right)\)
\(SA\in\left(SAB\right)\Rightarrow OJ||\left(SAB\right)\)
b. O là trung điểm BD, I là trung điểm BC
\(\Rightarrow OI\) là đườngt rung bình tam giác BCD
\(\Rightarrow OI||CD\)
Mà \(CD\in\left(SCD\right)\Rightarrow OI||\left(SCD\right)\)
Tương tự ta có IJ là đường trung bình tam giác SBC \(\Rightarrow IJ||SB\Rightarrow IJ||\left(SBD\right)\)
c. Ta có I là trung điểm BC, O là trung điểm AC
\(\Rightarrow M\) là trọng tâm tam giác ABC
\(\Rightarrow BM=\dfrac{2}{3}BO=\dfrac{2}{3}.\dfrac{1}{2}BD=\dfrac{1}{3}BD\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{1}{3}\)
Theo giả thiết \(SK=\dfrac{1}{2}KD=\dfrac{1}{2}\left(SD-SK\right)\Rightarrow SK=\dfrac{1}{3}SD\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}=\dfrac{BM}{BD}\Rightarrow KM||SB\) (Talet đảo)
\(\Rightarrow MK||\left(SBC\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 1
a.
Do M là trung điểm SA, O là trung điểm AC
\(\Rightarrow OM\) là đường trung bình tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\) (1)
N là trung điểm CD, O là trung điểm AC \(\Rightarrow ON\) là đường trung bình ACD
\(\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\) (2)
Mà \(ON\cap OM=O\) ; \(OM;ON\in\left(OMN\right)\) (3)
(1);(2);(3) \(\Rightarrow\left(OMN\right)||\left(SBC\right)\)
b.
J cách đều AB, CD \(\Rightarrow J\) thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O \(\Rightarrow OI\) là đường trung bình tam giác SBD \(\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)\)
Hay \(IJ||\left(SAB\right)\)
- Nếu J không trùng O, ta có \(\left\{{}\begin{matrix}IO||SB\left(đtb\right)\Rightarrow IO||\left(SAB\right)\\d||AB\Rightarrow IJ||AB\Rightarrow OJ||\left(SAB\right)\end{matrix}\right.\)
\(\Rightarrow\left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)\)
4 tháng 1
a.
Do M là trung điểm SA, O là trung điểm AC
là đường trung bình tam giác SAC (1)
N là trung điểm CD, O là trung điểm AC là đường trung bình ACD
(2)
Mà ; (3)
(1);(2);(3)
b.
J cách đều AB, CD thuộc đường thẳng d qua O và song song AB, CD
- Nếu J trùng O là đường trung bình tam giác SBD
Hay
- Nếu J không trùng O, ta có
CM
7 tháng 10 2017
Trong mặt phẳng (ABCD) ta có AC cắt BD tại O, IJ cắt BD tại E. trong mặt phẳng (SBD), ME cắt SO tại G. Ta có G thuộc (MIJ). (MIJ) chứa IJ // AC nên giao tuyến của (MIJ) với (SAC) là đường thẳng qua G và song song với AC.
Đáp án D
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
Ta có: \(SB=4MB=4\left(SB-SM\right)\Rightarrow\dfrac{SM}{SB}=\dfrac{3}{4}\)
Tương tự: \(\dfrac{SN}{SD}=\dfrac{3}{4}\)
\(\Rightarrow\dfrac{SM}{SB}=\dfrac{SN}{SD}\)
\(\Rightarrow MN||BD\) (định lý Talet đảo)
\(\Rightarrow BD||\left(MNP\right)\)
25 tháng 5 2017
Gọi K=AM∩SOK=AM∩SO. Mặt phẳng (P) đi qua K và song song với BD nên cắt (SBD) theo giao tuyế d' đi qua K và song song với BD. Vậy qua K, ta vẽ d' song song với BD. Đường thẳng d' cắt SB và SD lần lượt tại E và F. Đây là các điểm cần tìm.
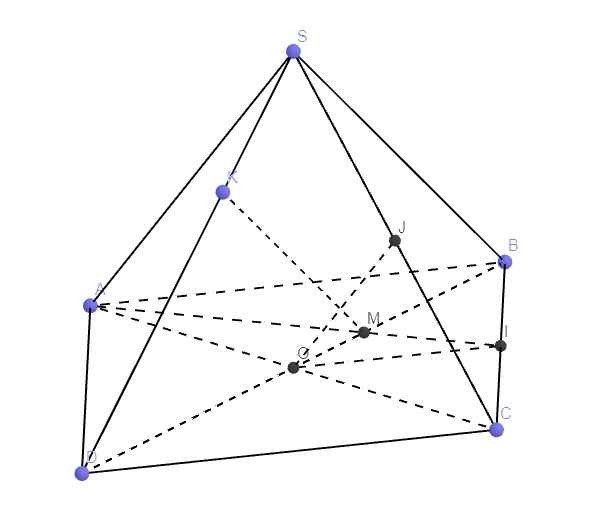
\(I=AN\cap BM\) nên I lần lượt thuộc hai mặt phẳng (SAC) và (SBD). Như vậy I phải thuộc giao tuyến SO của hai mặt phẳng này, ở đây \(O=AC\cap BD\). Tương tự, ta có J thuộc d