Cho hình chóp A.ABCD. Lấy M, N và P lần lượt là các điểm trên các đoạn SA, AB và BC sao cho chúng không trùng với trung điểm của các đoạn thẳng ấy. Tìm giao điểm (nếu có) của mặt phẳng (MNP) với các cạnh của hình chóp ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 12 2018
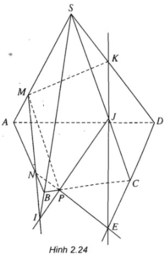
a lần lượt tìm giao điểm của mặt phẳng (MNP) với các đường thẳng chứa các cạnh của hình chóp.
Gọi I = MN ∩ SB
Ta có:
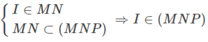
Vậy I = SB ∩ (MNP).
Từ đó, làm tương tự ta tìm được giao điểm của (MNP) với các cạnh còn lại.
Cụ thể :
Gọi J = IP ∩ SC, ta có J = SC ∩ (MNP)
Gọi E = NP ∩ CD, ta có E = CD ∩ (MNP)
Gọi K = JE ∩ SD, ta có K = SD ∩ (MNP)
CM
17 tháng 6 2017
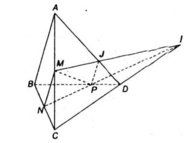
a) Ta có:
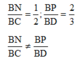
⇒ NP và CD không song song với nhau.
Gọi giao điểm NP và CD là I.
I ∈ NP ⇒ I ∈ (MNP).
Mà I ∈ CD
Vậy I ∈ CD ∩ (MNP)
b) Trong mặt phẳng (ACD) thì AD và MI cắt nhau tại điểm J:
J ∈ AD ⇒ J ∈ (ACD)
J ∈ MI ⇒ J ∈ (MNP)
Vậy J là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Ta đã có M là một điểm chung của hai mặt phẳng (ACD) và (MNP).
Vậy MJ = (ACD) ∩ (MNP).
D
25 tháng 9 2018
Bạn kham khảo tại link:
Cho hình chóp S.ABCD có đáy là hình bình hành tâm O. Gọi M, N, E là ba điểm lần lượt lấy trên AD, CD, SO. Tìm thiết diện của hình chóp bởi ( MNP) - Hình học không gian - Diễn đàn Toán học
Copy và dán:
https://diendantoanhoc.net/topic/125716-cho-h%C3%ACnh-ch%C3%B3p-sabcd-c%C3%B3-%C4%91%C3%A1y-l%C3%A0-h%C3%ACnh-b%C3%ACnh-h%C3%A0nh-t%C3%A2m-o-g%E1%BB%8Di-m-n-e-l%C3%A0-ba-%C4%91i%E1%BB%83m-l%E1%BA%A7n-l%C6%B0%E1%BB%A3t-l%E1%BA%A5y-tr%C3%AAn-ad-cd-so-t%C3%ACm-thi%E1%BA%BFt-di%E1%BB%87/
Học tốt!
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 12 2020
a.
Trong mp (SAB) nối PM kéo dài cắt SB tại G
Trong mp (ABCD) nối PN cắt BC kéo dài tại H
\(\Rightarrow GH=\left(MNP\right)\cap\left(SBC\right)\)
b.
Nối SE cắt AD tại I, nối SF cắt BC tại K
Trong mp (ABCD), nối IK cắt PN kéo dài tại S
Trong mp (SBC), SF kéo dài cắt GH tại R
\(\Rightarrow RS\) là giao tuyến của (MNP) và (SEF)
Trong mp (SEF), nối RS và EF cắt nhau tại Q
\(\Rightarrow Q=EF\cap\left(MNP\right)\)
Gọi \(J=IP\cap SC\), ta có \(J=SC\cap\left(MNP\right)\)
Gọi \(E=NP\cap CD\), ta có \(E=CD\cap\left(MNP\right)\)
Gọi \(K=JE\cap SD\), ta có \(K=SD\cap\left(MNP\right)\)