giải dùm em câu b bài 1 thôi được không ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2022
Cơ năng tại vị trí ban đầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\cdot8^2=32m\left(J\right)\)
a)Cơ năng tại nơi có độ cao cực đại:
\(W_1=mgh_{max}\left(J\right)\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow32m=mgh_{max}\Rightarrow h_{max}=\dfrac{32}{g}=\dfrac{32}{10}=3,2m\)
b)Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow32m=2mgz\Rightarrow z=\dfrac{32}{2g}=\dfrac{32}{2\cdot10}=1,6m\)
c)Cơ năng tại nơi \(W_t=\dfrac{1}{4}W_đ\Rightarrow W_đ=4W_t\):
\(W_3=5W_t=5mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow32m=5mgz'\Rightarrow z'=\dfrac{32}{5g}=\dfrac{32}{5\cdot10}=0,64m\)
13 tháng 5 2016
Bạn yên tâm, các câu trả lời của bạn sẽ được kiểm duyệt hết
DT
2
25 tháng 2 2022
Bài 2.
Tóm tắt:
\(v=6\)m/s, \(g=10\)m/s2
a)\(h_{max}=?\)
b)\(W_t=W_đ\Rightarrow z=?\)
c)\(W_đ=2W_t\Rightarrow z'=?\)
Giải chi tiết:
Cơ năng tại vị trí ban đầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\cdot6^2=18m\left(J\right)\)
a)Tại nơi có độ cao \(h_{max}\): \(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\)
\(\Rightarrow h_{max}=\dfrac{18}{g}=\dfrac{18}{10}=1,8m\)
b)Tại nơi thế năng bằng động năng thì cơ năng là
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\)
\(\Rightarrow z=\dfrac{18}{2g}=\dfrac{9}{10}=0,9m\)
c)Tại nơi động năng bằng hai lần thế năng:
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{6}{10}=0,6m\)
25 tháng 2 2022
Bài 3.
a)Cơ năng ban đầu: \(W=W_đ+W_t\)
\(\Rightarrow W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}m\cdot0^2+m\cdot10\cdot20=200m\left(J\right)\)
Cơ năng tại nơi vận tốc vật khi cham đất:
\(W'=\dfrac{1}{2}mv'^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow200m=\dfrac{1}{2}mv'^2\)
\(\Rightarrow v'=20\)m/s
Cách khác nè:Áp dụng công thức( chỉ sử dụng khi tính vận tôc vật chạm đất)
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot20}=20\)m/s
b)Tại nơi có thế năng bằng động năng thì cơ năng là:
\(W_1=W_t+W_đ=2W_t=2mgh\)
Bảo toàn cơ năng: \(W_1=W\)
\(\Rightarrow2mgh=200m\)
\(\Rightarrow h=10m\)
c)Cơ năng tại nơi thế năng gấp 3 động năng:
\(W_2=W_đ+W_t=W_đ+3W_đ=4W_đ=4\cdot\dfrac{1}{2}mv'^2=2mv'^2\)
Bảo toàn cơ năng: \(W_2=W\)
\(\Rightarrow200m=2mv'^2\)
\(\Rightarrow v'=10\)m/s
DT
1
27 tháng 2 2022
Câu 2.
Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot m\cdot6^2+m\cdot10\cdot0=18m\left(J\right)\)
a)Cơ năng tại nơi có độ cao cực đại:
\(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\Rightarrow h_{max}=\dfrac{18}{10}=1,8m\)
b)Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\Rightarrow z=\dfrac{18}{2g}=\dfrac{18}{2\cdot10}=0,9m\)
c)Cơ năng tại nơi \(W_đ=2W_t\):
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{18}{3\cdot10}=0,6m\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
23.
\(\Delta'=m^2-\left(m^2-1\right)=1>0;\forall m\)
\(\Rightarrow\) Pt luôn có 2 nghiệm pb với mọi m
24.
Pt đã cho có 2 nghiệm trái dấu khi:
\(ac< 0\Leftrightarrow\left(m^2+2020\right)\left(m-2021\right)< 0\)
\(\Leftrightarrow m< 2021\Rightarrow\) có 2020 giá trị nguyên dương
25.
\(y=4x^2-3+\dfrac{9}{x^2}=4x^2+\dfrac{9}{x^2}-3\ge2\sqrt{4x^2.\dfrac{9}{x^2}}-3=9\)
30 tháng 8 2021
Bài 2:
a: Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin50^0\)
\(\Leftrightarrow AB\simeq30,64\left(cm\right)\)
\(\Leftrightarrow AC=\sqrt{40^2-30.64^2}\simeq25,71\left(cm\right)\)
C1
2
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
29.
Do \(M\in\Delta\) nên tọa độ có dạng: \(M\left(m;2m+1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=\left(m-4;2m+4\right)\\\overrightarrow{BM}=\left(m-5;2m-4\right)\\\overrightarrow{CM}=\left(m-1;2m+2\right)\end{matrix}\right.\)
\(\Rightarrow AM^2+BM^2+CM^2\)
\(=\left(m-4\right)^2+\left(2m+4\right)^2+\left(m-5\right)^2+\left(2m-4\right)^2+\left(m-1\right)^2+\left(2m+2\right)^2\)
\(=15m^2-12m+78\)
\(=15\left(m-\dfrac{2}{5}\right)^2+\dfrac{378}{5}\ge\dfrac{378}{5}\)
Dấu "=" xảy ra khi \(m=\dfrac{2}{5}\Rightarrow M\left(\dfrac{2}{5};\dfrac{9}{5}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 1 2022
30.
Đặt \(f\left(x\right)=x^2-6x-7\)
Đồ thị hàm \(y=\left|f\left(x\right)\right|=\left|x^2-6x-7\right|\) được tạo ra bằng cách lấy đối xứng phần bên dưới trục Ox của đồ thị \(f\left(x\right)\) lên như hình vẽ:
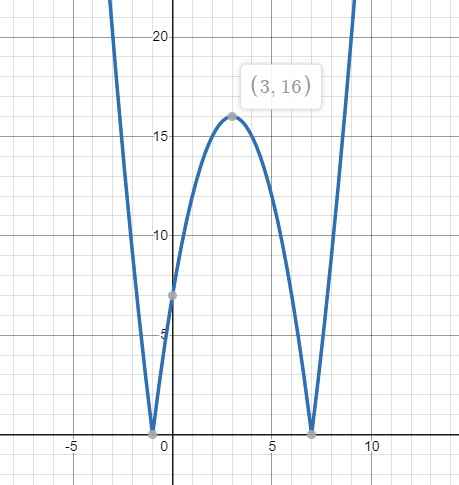
Từ đồ thị ta thấy pt có 4 nghiệm pb khi và chỉ khi: \(0< m< 16\)
\(\Rightarrow\) Có 15 giá trị nguyên của m
C1
1
Bài 1:
b: Ta có: \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}-\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(-\sqrt{7}+\sqrt{5}\right)\cdot\left(\sqrt{7}+\sqrt{5}\right)\)
=5-7
=-2
b) \(\left(\dfrac{\sqrt{14}-\sqrt{7}}{1-\sqrt{2}}-\dfrac{\sqrt{15}-\sqrt{5}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{-\left(\sqrt{2}-1\right)}-\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{-\left(\sqrt{3}-1\right)}\right):\dfrac{1}{\sqrt{7}+\sqrt{5}}\)
\(=\left(\sqrt{5}-\sqrt{7}\right).\left(\sqrt{5}+\sqrt{7}\right)\)
\(=5-7\\ =-2\)