cho hình thang vuông ABCD , AB = 4cm, DC = 9cm, BC = 13cm. Tính khoảng cách từ trung điểm M của AD đến BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 3 2022
a) -Qua B kẻ đường thẳng vuông góc với DC tại E.
-Xét tứ giác ABED: \(\widehat{ADE}=\widehat{BAD}=\widehat{DEB}=90^0\)
\(\Rightarrow\)ABED là hình chữ nhật nên \(AD=BE\); \(AB=ED=4\left(cm\right)\)
-Xét △BEC vuông tại E:
\(BE^2+EC^2=BC^2\) (định lí Py-ta-go)
\(\Rightarrow BE^2+\left(DC-DE\right)^2=BC^2\)
\(\Rightarrow BE^2+\left(9-4\right)^2=13^2\)
\(\Rightarrow BE^2=13^2-5^2=144\)
\(\Rightarrow BE=AD=12\left(cm\right)\)
b) \(S_{ABCD}=\dfrac{AD.\left(AB+CD\right)}{2}=\dfrac{12.\left(4+9\right)}{2}=78\left(cm^2\right)\)
c) -Đề sai.
CM
30 tháng 10 2018
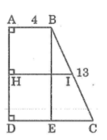
Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
B C 2 = B E 2 + C E 2
Suy ra : B E 2 = B C 2 - C E 2 = 13 2 - 5 2 = 144
BE = 12 (cm)
Vậy: AD = 12 (cm)