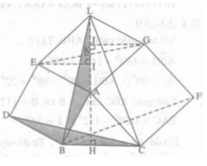
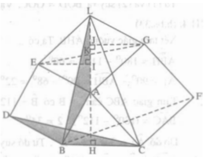
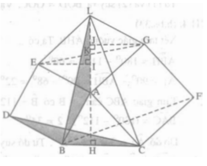
Dựng các hình vuông ABDE và ACFG bên ngoài tam giác nhọn ABC cho trước.
a) Gọi H là điểm thuộc đường thẳng BC sao cho \(AH\perp BC\). Gọi I, J là các điểm thuộc đường thẳng AH sao cho \(EI\perp AH\) và \(GJ\perp AH\). Chứng minh :
\(\Delta ABH=\Delta EAI,\Delta ACH=\Delta GAJ\)
Từ đó suy ra đường thẳng AH cắt EG tại trung điểm K của EG (tức là AK là trung tuyến của tam giác AEG)
b) Gọi L là điểm thuộc đường thẳng AK sao cho K là trung điểm của AL. Chứng minh AL = BC
c) Chứng minh \(\Delta ABL=\Delta BDC\). Từ đó suy ra CD là một đường cao của tam giác BCL
d) Chứng minh rằng các đường thẳng AH, BF, CD đồng quy ?

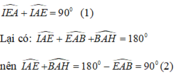
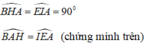
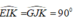
Bài này vẽ hình hơi dài dòng mà em ko bt vẽ hình ở H24 HOC24
Thôi thì lời giải của em ở trang 98->99
Hình bs.36