Question

[Đỗ Thị Kim Anh]

\(cho\Delta\) ABC vuông tại A, đường cao AM. biết BC= 15cm, BM= 6cm. đường trung trực của BC cắt AC tại E cắt BC tại F. chứng minh:

a, \(\Delta\) ABC đồng dạng với \(\Delta\) ABM

b,\(\Delta\) AMB đồng dạng với \(\Delta\)CMA

c, tính AM và AB

d, tính tỉ số diện tích \(\Delta\) EFC và \(\Delta\)BAC

( viết giả thiết , kết luận , chứng minh)

Answer 1

[Xuân Tuấn Trịnh]

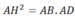
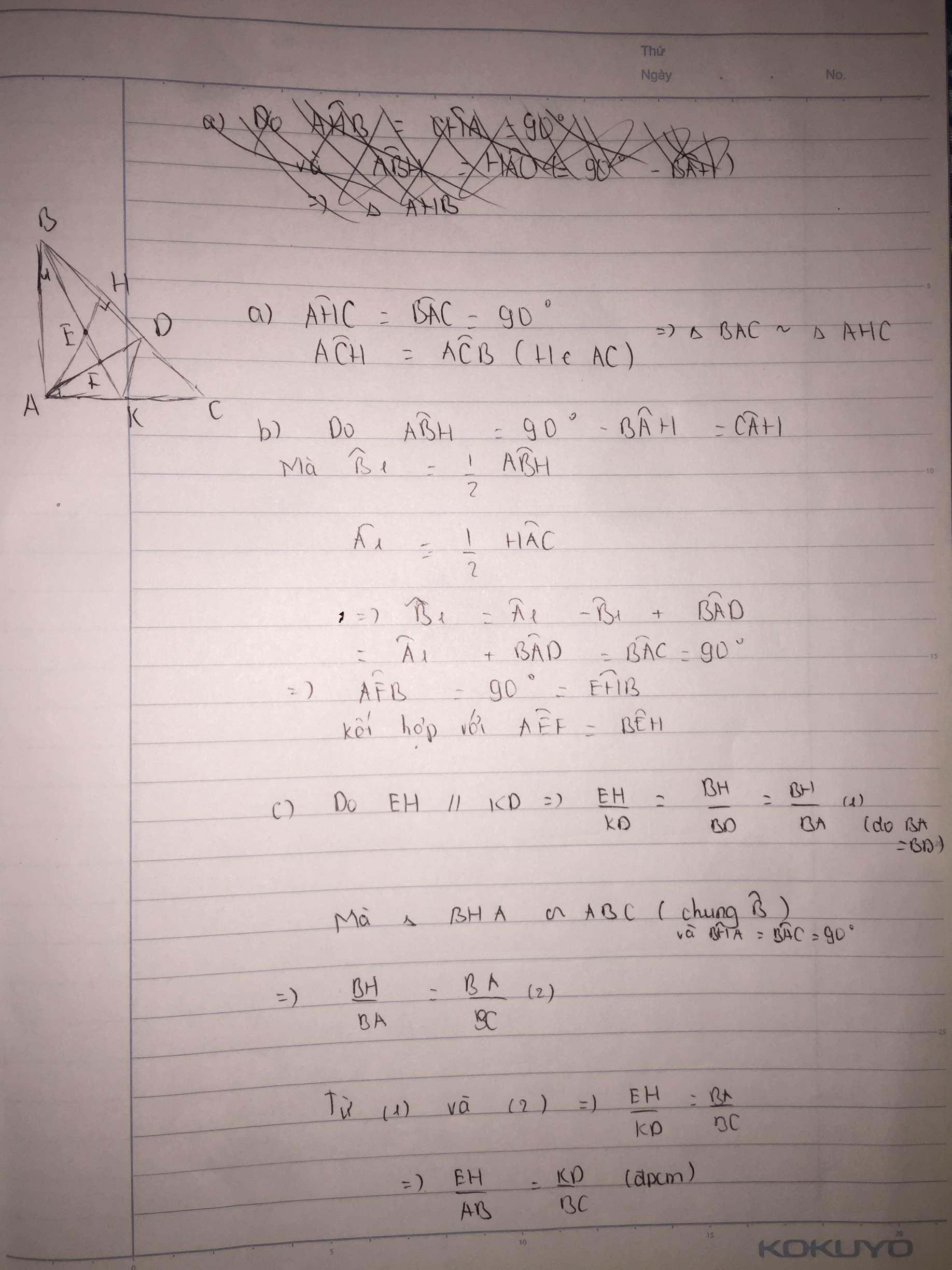
a)Xét tam giác ABC và tam giác MBA có:

góc BAC = góc BMA(=90^o do AM là đường cao và tam giác ABC vuông)

Góc ABC chung

=>\(\Delta ABC\infty\Delta MBA\)(g.g)(1)

b)Xét tam giác ABC và tam giác MAC có:

Góc ACB chung

góc BAC = góc AMC(=90⁰)

=>\(\Delta ABC\infty\Delta MAC\)(g.g)(2)

Từ 1 và 2 =>\(\Delta MBA\infty\Delta MAC\) hay \(\Delta AMB\infty\Delta CMA\)

c)\(\Delta AMB\infty\Delta CMA\)=>\(\dfrac{AM}{CM}=\dfrac{BM}{AM}\)

=>AM²=BM.CM

Mà BM+CM=BC,BC=15cm BM=6cm=>CM=9cm

=>AM²=6.9=54

=>AM=\(3\sqrt{6}\)(cm)

Áp dụng định lí pytago cho tam giác AMB ta có:

AB²=AM²+BM²=54+6²=90

=>AB=\(3\sqrt{10}\)(cm)

d)S_AFC=1/2 S_ABC(chung đường cao từ A đáy FC=1/2 BC do F nằm trên trung trực BC và F thuộc BC)

Ta có:FB=FB=\(\dfrac{BC}{2}=7,5\left(cm\right)\)

AM//FE do cùng vuông góc với BC

=>\(\dfrac{CF}{CM}=\dfrac{CE}{CA}\)

=>\(\dfrac{CE}{CA}=\dfrac{7,5}{9}=\dfrac{5}{6}\)

=>S_EFC=\(\dfrac{5}{6}\)S_AFC(chung đường cao từ F và EC=\(\dfrac{5}{6}CA\))

=>S_EFC=(\(\dfrac{5}{6}\cdot\dfrac{1}{2}\))S_ABC=\(\dfrac{5}{12}\)S_ABC