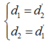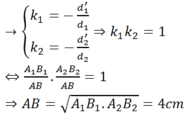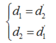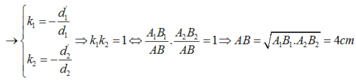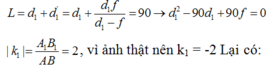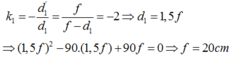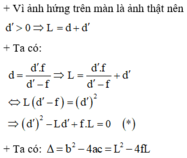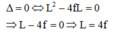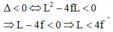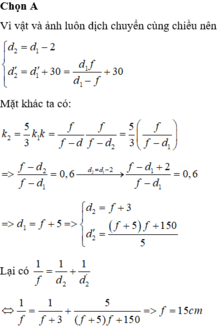cho vật sáng AB cao 4cm đặt sông song với màn cánh màn một khoảng 45cm luôn không đổi, giữa màn và vật đặt một thấu kính hội tụ, A nằm trên trục chính của thấu kính, trên màn hứng được ảnh A1B1. Nếu đổi vị trí giữa vật và màn cho nhau thì trên màn có ảnh A2B2 lớn gấp 4 lần A1B1.
Xách định tiêu cự của thấu kính