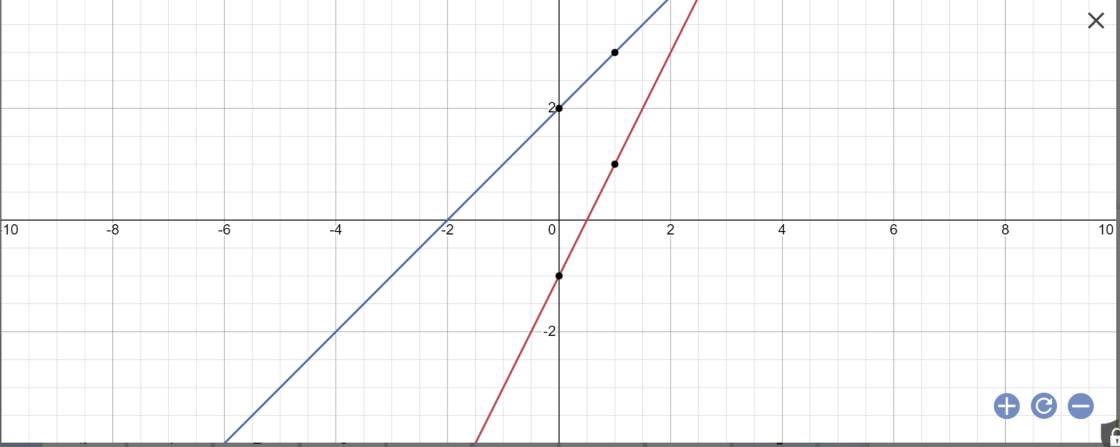
Tìm giao điểm của hai đường thẳng:a) \(\left(d_1\right):5x-2y=c,\left(d_2\right):x by=2\), biết rằng \(\left(d

SG

Sách Giáo Khoa

6 tháng 5 2017

Tìm giao điểm của hai đường thẳng:a) \(\left(d_1\right):5x-2y=c,\left(d_2\right):x+by=2\), biết rằng \(\left(d_1\right)\) đi qua điểm \(A\left(5;-1\right)\) và \(\left(d_2\right)\) đi qua điểm \(B\left(-7;3\right)\).b) \(\left(d_1\right):ax+2y=-3,\left(d_2\right):3x-by=5\), biết rằng \(\left(d_1\right)\) đi qua điểm \(M\left(3;9\right)\) và \(\left(d_2\right)\) đi qua...

Đọc tiếp

#Toán lớp 9

1

NT

Nguyen Thuy Hoa

16 tháng 6 2017

Hệ hai phương trình bậc nhất hai ẩn

Đúng(0)

HA

hải anh thư hoàng

29 tháng 8 2023

Bài 1: Cho 2 đường thẳng \(\left(d_1\right)y=2x-1\); \(\left(d_2\right)y=x+2\)a, Vẽ 2 đường thẳng \(\left(d_1\right)\)và \(\left(d_2\right)\) trên cùng 1 mặt phẳng tọa độ b, Xác định tọa độ giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\) bằng phép toánc, Viết phương trình đường thẳng \(\left(d\right)y=ax+b\). Biết \(\left(d\right)//\left(d_1\right)\) và cắt trục hoành tại điểm có hoành độ bằng...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

29 tháng 8 2023

a: loading...

b: Phương trình hoành độ giao điểm là:

2x-1=x+2

=>x=3

Thay x=3 vào y=x+2, ta được:

y=3+2=5

c: Vì (d)//(d1) nên (d): y=2x+b

Thay x=1 và y=0 vào (d), ta được:

b+2=0

=>b=-2

=>y=2x-2

Đúng(0)

TB

Tạ Bla Bla

31 tháng 12 2021

Cho hai đường thẳng \(y=-4x+m-1\left(d_1\right)\) và \(y=\dfrac{4}{3}x+15-3x\left(d_2\right)\)a, Tìm m để đường thẳng \(\left(d_1\right)\) và (\(\left(d_2\right)\) cắt nhau tại một điểm C trên trục tung.b, Với m ở trên hãy tìm tọa độ giao điểm A,B của 2 đường thẳng \(\left(d_1\right),\left(d_2\right)\) với trục...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

31 tháng 12 2021

b: Để hai đường thẳng cắt nhau tại một điểm trên trục tung thì m-1=15

hay m=16

Đúng(0)

SG

Sách Giáo Khoa

5 tháng 5 2017

Vẽ hai đường thẳng \(\left(d_1\right):x+y=2\) và \(\left(d_2\right):2x+3y=0\)

Hỏi đường thẳng \(\left(d_3\right):3x+2y=10\) có đi qua giao điểm của \(\left(d_1\right)\) và \(\left(d_2\right)\) hay không?

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

17 tháng 5 2022

Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}x+y=2\\2x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\y=-4\end{matrix}\right.\)

Thay x=6 và y=-4 vào (d3), ta được:

\(3\cdot6+2\cdot\left(-4\right)=10\left(đúng\right)\)

Vậy: (d3) đi qua giao điểm của (D1) và (D2)

Đúng(0)

TV

trần vũ hoàng phúc

27 tháng 12 2023

Tìm quỹ tích giao điểm của hai đường thẳng \(\left(d_1\right):mx+2y=m+1\) và \(\left(d_2\right):2x+my=2m-1\)

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

29 tháng 12 2023

Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}mx+2y=m+1\\2x+my=2m-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2mx+4y=2m+2\\2mx+m^2y=2m^2-m\end{matrix}\right.0\Leftrightarrow\left\{{}\begin{matrix}2mx+m^2y-2mx-4y=2m^2-m-2m-2\\mx+2y=m+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y\left(m^2-4\right)=2m^2-3m-2\\mx+2y=m+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y\left(m-2\right)\left(m+2\right)=\left(m-2\right)\left(2m+1\right)\\mx+2y=m+1\end{matrix}\right.\)(1)

TH1: m=2

Hệ phương trình (1) sẽ trở thành:

\(\left\{{}\begin{matrix}y\left(2-2\right)\left(2+2\right)=\left(2-2\right)\left(2\cdot2+1\right)\\2x+2y=2+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}0y=0\\2x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y\in R\\2x+2y=3\end{matrix}\right.\)

Vậy: Khi m=2 thì (d1) và (d2) trùng nhau

TH2: m=-2

Hệ phương trình (1) sẽ trở thành:

\(\left\{{}\begin{matrix}y\cdot\left(-2-2\right)\left(-2+2\right)=\left(-2-2\right)\left(-2\cdot2+1\right)\\-2x+2y=-2+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}0y=\left(-4\right)\cdot\left(-3\right)=12\\-2x+2y=-1\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\varnothing\)

Vậy: Khi m=-2 thì (d1)//(d2)

TH3: \(m\notin\left\{2;-2\right\}\)

hệ phương trình (1) sẽ trở thành:

\(\left\{{}\begin{matrix}y=\dfrac{\left(m-2\right)\left(2m+1\right)}{\left(m-2\right)\left(m+2\right)}=\dfrac{2m+1}{m+2}\\mx+2y=m+1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=\dfrac{2m+1}{m+2}\\mx=m+1-\dfrac{4m+2}{m+2}=\dfrac{\left(m+1\right)\left(m+2\right)-4m-2}{m+2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=\dfrac{2m+1}{m+2}\\x=\dfrac{m^2+3m+2-4m-2}{m\left(m+2\right)}=\dfrac{m^2-m}{m\left(m+2\right)}=\dfrac{m-1}{m+2}\end{matrix}\right.\)

vậy: Khi \(m\notin\left\{2;-2\right\}\) thì (d1) cắt (d2) tại \(A\left(\dfrac{m-1}{m+2};\dfrac{2m+1}{m+2}\right)\)

Đúng(2)

NT

Nguyễn Thị Thu Hằng

26 tháng 2 2020

Cho hàm số y=-x+3 \(\left(d_1\right)\) và y=3x-1 \(\left(d_2\right)\) a, Vẽ \(\left(d_1\right)\) và \(\left(d_2\right)\) b, Tìm tọa độ giao điểm \(d_1\) và \(d_2\) c, Lập phương trình đường thẳng đi qua điểm (2;-5) và song song với...

Đọc tiếp