Cho tam giác vuông ABC (\(\widehat{A}=90^0\) ). Dựng AD vuông góc với BC (D thuộc BC). Đường phân giác BE cắt AD tại F (h.29)
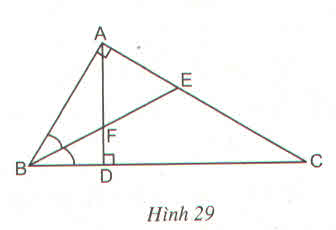
Chứng minh :
\(\dfrac{FD}{FA}=\dfrac{EA}{EC}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
5 tháng 7 2017
Đúng(0)
Những câu hỏi liên quan
10 tháng 5 2023
a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
góc C chung
=>ΔHAC đồng dạng vói ΔABC
b: \(AB=\sqrt{5^2-3^2}=4\left(cm\right)\)
AH=3*4/5=2,4cm
HB=4^2/5=3,2cm
c: FH/FA=BH/BA
EA/EC=BA/BC
BH/BA=BA/BC
=>FH/FA=EA/EC
29 tháng 8 2021
a: Ta có: ΔABC cân tại A
mà AD là đường phân giác ứng với cạnh đáy BC
nên AD là đường cao ứng với cạnh BC
Xét ΔABC có
AD là đường cao ứng với cạnh BC
BE là đường cao ứng với cạnh AC
AD cắt BE tại H
Do đó: H là trực tâm của ΔBAC
Suy ra: CH\(\perp\)AB
29 tháng 8 2021
Cảm ơn bạn!
Nhưng mình biết làm câu a với b rồi bạn làm cho mình câu c với d với
30 tháng 5 2021
a)xét ΔBAD và ΔBCE có
\(\widehat{ADB}=\widehat{CEB}=90^o\)
\(\widehat{ABC}\) là góc chung
AB=BC(ΔABC cân tại B)
⇒ ΔBAD=ΔBCE(c.huyền.g.nhọn)
b)xét ΔEBF và ΔDBF có:
BF là cạnh chung
BD=BE(ΔBAD=ΔBCE)
\(\widehat{BDF}=\widehat{BEF}=90^o\)
⇒ΔEBF=ΔDBF(c.huyền.c.g.vuông)
⇒\(\widehat{EBF}=\widehat{DBF}\)(2 góc tương ứng)
hay BF là phân giác của \(\widehat{ABC}\)(đ.p.cm)
c)xét ΔABF và ΔCBF có:
AC=BC(ΔABC cân tại B)
BF là cạnh chung
\(\widehat{EBF}=\widehat{DBF}\)(ΔEBF=ΔDBF)
⇒ΔABF=ΔCBF(c-g-c)
⇒FA=FC(2 cạnh tương ứng)
xét ΔAFC có:
FA+FC>AC(bất đẳng thức tam giác)
mà FA=FC⇒FA>\(\dfrac{AC}{2}\)(đ.p.cm)