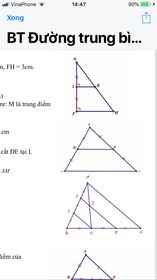
Bài 4: Cho hình vẽ bên. a) Cmr: I là trung điểm AD b) Cmr: FI=1/8 AC
Hình thứ 3 nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có: \(GI=IF=\dfrac{GF}{2}\) ( do I là trung điểm GF)
\(\Rightarrow GI=GF=\dfrac{4}{2}=2\left(cm\right)\)
Xét ΔABC có:
I là trung điểm của GF(gt)
IK//FH(gt)
=> K là trung điểm của GH
=> IK là đường trung bình của tam giác ABC
=> \(IK=\dfrac{1}{2}FH=\dfrac{1}{2}.3=\dfrac{3}{2}\)(cm)
Xét tam giác GIK vuông tại I có:
\(GK^2=GI^2+IK^2\)( định lý Pytago)
\(\Rightarrow GK=\sqrt{GI^2+IK^2}=\sqrt{2^2+\left(\dfrac{3}{2}\right)^2}=\dfrac{5}{2}\left(cm\right)\)
b) Xét tam giác KGF có:
\(KI\perp GF\)( KI //FH, FH⊥GF=> KI⊥GF)
KI là đường trung tuyến( I là trung điểm của GF)
=> Tam giác KGF cân tại K
c) Cách 1:
Xét tam giác GCH vuông tại C có
FK là đường trung tuyến ứng với cạnh huyền GH( K là trung điểm của GH)
=> \(FK=\dfrac{1}{2}GH=KH\) \(\Rightarrow\Delta FKH\) cân tại K
Cách 2:
Xét tam giác GFH có:
IK là đường trung bình
=> IK//FH \(\Rightarrow\left\{{}\begin{matrix}\widehat{IKF}=\widehat{KFH}\\\widehat{GKI}=\widehat{KHF}\end{matrix}\right.\)
Mà \(\widehat{GKI}=\widehat{IKF}\) ( do tam giác GKF cân tại K nên KI là tia phân giác \(\widehat{GKF}\))
\(\Rightarrow\widehat{KFH}=\widehat{KHF}\Rightarrow\Delta KFH\) cân tại K
d) Cách 1:
Xét tam giác KFH cân tại K có:
KM là đường cao ( KM⊥FH)
=>KM là đường trung tuyến => M là trung điểm của FH
Cách 2:
Xét tứ giác IKMF có:
\(\widehat{KIF}=\widehat{IFM}=\widehat{FMK}=90^0\) => Tứ giác IKMF là hình chữ nhật
=> IK =FM mà \(FM=\dfrac{1}{2}FH\Rightarrow IK=\dfrac{1}{2}FH\Rightarrow M\) là trung điểm của FH
Cách 3:
Xét tam giác GFH có:
K là trung điểm của GH(IK là đường trung bình)
KM//GF( cùng vuông góc với FH)
=> M là trung điểm của FH
e) Xét tam giác GCH vuông tại C có:
\(GH^2=GC^2+CH^2\Rightarrow GH=\sqrt{GC^2+CH^2}=\sqrt{4^2+3^2}=5\left(cm\right)\)
Ta có: Tứ giác IKMF là hình chữ nhật
\(\Rightarrow IM=FK=\dfrac{1}{2}GH=\dfrac{1}{2}.5=\dfrac{5}{2}\left(cm\right)\)

Bài 3:
a: Xét ΔCDF vuông tại C và ΔBCE vuông tại B có
CD=BC
CF=BE
Do đó: ΔCDF=ΔBCE
=>góc CDF=góc BCE
=>góc BCE+góc MFC=góc DFC+góc CDF=90 độ
=>CE vuông góc với DF
b: Gọi Klà trung điểm của CD và N là giao của AK và DF
Xét tứ giác AECK có
AE//CK
AE=CK
Do dó: AECK là hình bình hành
SUy ra: AK=CE và AK//CE
=>AK vuông góc với DF
Xét ΔDMC có
K là trung điểm của DC
KN//MC
Do đó: N là trung điểm của DM
Xét ΔAMD có
AN vừa là đường cao, vừa là đường trung tuyến
nên ΔAMD cân tại A

câu 2
tam giác ABM bằng tam giác DBN (c.g.c) nên BM=BN và ABM=DBN ta có ABM+MBD=60 nên DBN+MBD=60 hay MBN =60 tam giác MBN đều