Cho tam giác DEF vuông tại E có DE=15cm, EF=20cm, đường cao EH.
a) Chứng minh: EH.DF=ED.EF. Tính DF, EH? b) Kẻ HM vuông góc với ED, HN vuông góc với EF. Chứng minh tam giác EMN đồng dạng với tam giác EFD. c) Trung tuyến EK của tam giác DEF cắt MN tại I. Tính diện tích tam giác EIM.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 6 2022
a: \(S_{DEF}=\dfrac{EH\cdot DF}{2}=\dfrac{ED\cdot EF}{2}\)
nên \(EH\cdot DF=ED\cdot EF\)
b: \(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
c: Xét ΔDEF vuông tại E có EH là đường cao
nên \(EF^2=DF\cdot HF\)
d: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
Xét ΔEMN và ΔEFD có
EM/EF=EN/ED
góc MEN chung
Do đo: ΔEMN đồng dạng với ΔEFD
3 tháng 5 2020
Bài làm
a) Xét tam giác DEH và tam giác DEF có:
\(\widehat{DHE}=\widehat{DEF}\left(=90^0\right)\)
\(\widehat{D}\) chung
=> Tam giác DEH ~ Tam giác DEF ( g - g )
=> \(\frac{DE}{DF}=\frac{HE}{EF}\)
\(\Rightarrow DE.EF=DF.EH\) ( đpcm )
b) Xét tam giác DEF vuông tại E có:
DF2 = DE2 + EF2
hay DF2 = 152 + 202
=> DF2 = 225 + 400
=> DF2 = 625
=> DF = 25 ( cm )
Vì tam giác DEH ~ Tam giác DEF ( cmt )
=> \(\frac{DH}{DE}=\frac{DE}{DF}\)
hay \(\frac{DH}{15}=\frac{15}{25}\Rightarrow DH=9\left(cm\right)\)
Ta có: DH + HF = DF
hay 9 + HF = 25
=> HF = 16 ( cm )
c) Xét tam giác HEF và tam giác EDF có:
\(\widehat{EHF}=\widehat{DEF}\left(=90^0\right)\)
\(\widehat{F}\) chung
=> Tam giác HEF ~ Tam giác EDF ( g - g )
=> \(\frac{EF}{DF}=\frac{HF}{EF}\Rightarrow EF^2=DF.HF\) ( đpcm )
31 tháng 1
a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
TT
15 tháng 5 2021
a) xét ΔHED và ΔDEF có
\(\widehat{EHD}=\widehat{EDF}=\)90o
\(\widehat{E} chung\)
=> ΔHED ∼ ΔDEF (gg)
b) Xét ΔDEF có \(\widehat{D}=\)90o
=> DE2+DF2=EF2
=>62+82=EF2
=> EF=10 cm
SΔDEF=\(\dfrac{ED.DF}{2}=\dfrac{DH.EF}{2}\)=> ED.DF=DH.EF => 6.8=DH.10
=> DH =4,8 cm
c) Xét ΔDEH có \(\widehat{EHD}=90\)o
=> HD2.HE2=ED2
=>4.82+HE2=62
=> HE=3.6
ta lại có DI là phân giác
=> \(\dfrac{EI}{IH}=\dfrac{ED}{HD}\)
=>\(\dfrac{EI}{EH-EI}=\dfrac{6}{4.8} \)=>\(\dfrac{EI}{3.6-EI}=\dfrac{6}{4.8}\)=>EI=2
=> IH=EH-EI=3.6-2=1.6
15 tháng 5 2021
a) Xét ΔHED vuông tại H và ΔDEF vuông tại D có
\(\widehat{HED}\) chung
Do đó: ΔHED\(\sim\)ΔDEF(g-g)
26 tháng 3 2023
\(\text{#TNam}\)
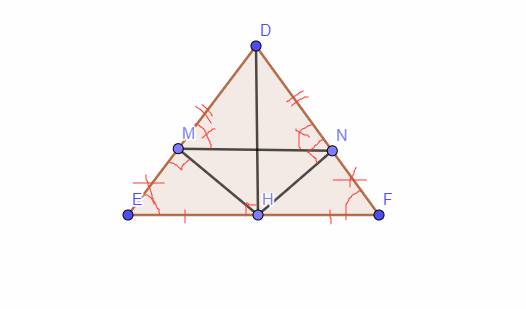
`a,` Xét Tam giác `HED` và Tam giác `HFD` có
`DE = DF (\text {Tam giác DEF cân tại D})`
\(\widehat{E}=\widehat{F}\) `(\text {Tam giác DEF cân tại D})`
`=> \text {Tam giác HED = Tam giác HDF (ch-gn)}`
`b,` Vì Tam giác `HED =` Tam giác `HFD (a)`
`-> HE = HF (\text {2 cạnh tương ứng})`
Xét Tam giác `HEM` và Tam giác `HFN` có:
`HE = HF (CMT)`
\(\widehat{E}=\widehat{F}\) `(a)`
\(\widehat{EMH}=\widehat{FNH}=90^0\)
`=> \text {Tam giác HEM = Tam giác HFN (ch-gn)}`
`-> EM = FN (\text {2 cạnh tương ứng})`
Ta có: \(\left\{{}\begin{matrix}DE=MD+ME\\DF=ND+NF\end{matrix}\right.\)
Mà `DE = DF, ME = NF`
`-> MD = ND`
Xét Tam giác `DMN: DM = DN (CMT)`
`-> \text {Tam giác DMN cân tại D}`
`->`\(\widehat{DMN}=\widehat{DNM}=\)\(\dfrac{180-\widehat{A}}{2}\)
Tam giác `DEF` cân tại `D`
`->`\(\widehat{E}=\widehat{F}=\)\(\dfrac{180-\widehat{A}}{2}\)
`->`\(\widehat{DMN}=\widehat{E}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {MN // EF (t/c 2 đt' //)}`
a: Xét ΔDEF vuông tại E cso EH là đường cao
nên \(EH\cdot DF=ED\cdot EF\)(hệ thức lượng)
\(DF=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(EH=\dfrac{ED\cdot EF}{DF}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
b: Xét ΔEHD vuông tại H có HM là đường cao
nên \(EM\cdot ED=EH^2\left(1\right)\)
Xét ΔEHF vuông tại H có HN là đường cao
nên \(EN\cdot EF=EH^2\left(2\right)\)
Từ (1) và (2) suy ra \(EM\cdot ED=EN\cdot EF\)
hay EM/EF=EN/ED
Xét ΔEMN vuông tại E và ΔEFD vuông tại E có
EM/EF=EN/ED
Do đó ΔEMN\(\sim\)ΔEFD