Cho góc vuông xOy, điểm A trên tia Oy. Điểm B di chuyển trên tia Ox. Gọi C là điểm đối xứng với A qua B. Điểm C di chuyển trên đường nào ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


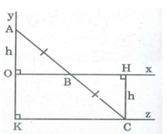
Vì điểm C đối xứng với điểm A qua điểm B nên BA = BC
Kẻ CH ⊥ Ox
Xét hai tam giác vuông AOB và CHB, ta có:
∠ (AOB) = ∠ (CHB ) = 90 0
BA = BC ( chứng minh trên)
∠ (ABO ) = ∠ (CBH) ( đối đỉnh)
Suy ra ∆ AOB = ∆ CHB ( cạnh huyền, góc nhọn)
⇒ CH = AO
Vì A, O cố định nên OA không đổi suy ra CH không đổi
Vì C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng bằng OA.
Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.
Vậy C chuyển động trên tia Kz // Ox, cách Ox một khoảng không đổi bằng OA.

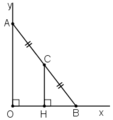
- Cách 1:
Kẻ CH ⊥ Ox.
Ta có CB = CA (gt).
CH // AO (cùng vuông góc Ox)
⇒ HB = OH
⇒ CH là đường trung bình của tam giác AOB
⇒ CH = AO/2 = 1cm.
Điểm C cách tia Ox cố định một khoảng không đổi 1cm nên C di chuyển trên tia song song với Ox, cách Ox một khoảng bằng 1cm và nằm trong góc xOy.
- Cách 2:
Vì C là trung điểm của AB nên OC là trung tuyến ứng với cạnh huyền AB do đó OC = CA.
Điểm C di chuyển trên tia Em thuộc đường trung trực của OA.
m:
Kẻ CH vuông góc với Ox
Ta có: CB = CA (gt) và CH // AO (cùng vuông góc với Ox)
⇒ CH = 12AO = 12.2 = 1 (cm)
Điểm C cách tia Ox cố định một khoảng không đổi 1cm nên điểm C di chuyển trên đường thẳng m song song với Ox và cách Ox một khoảng

Cách 1:
Kẻ CH ⊥ Ox
Ta có CB = CA (gt)
CH // AO (cùng vuông góc Ox)
Suy ra CH = 1212AO = 1212.2 = 1 (cm)
Điểm c cách tia Ox cố định một khoảng không đổi 1cm nên C di chuyển trên tia Em song song với Ox và cách Ox một khoảng bằng 1cm.
Cách 2:
Vì C là trung điểm của AB nên OC là trung tuyến ứng với cạnh huyền AB
do đó CO = CA
Điểm C di chuyển trên tia Em thuộc đường trung trực của OA
mình vẫn chưa hiểu c2 cho lắm
tại sao lại là đương trung trực?
đúng mình cho 2 like


Vì điểm C đối xứng với điểm A qua điểm B ⇒ BA = BC
Kẻ CH ⊥ Ox
Xét ∆ AOB và ∆ CHB ta có :
\(\widehat{AOB}=\widehat{CHB}=90^o\)
\(BA=BC\left(cmt\right)\)
\(\widehat{ABO}=\widehat{CBH}\) ( đối đỉnh )
\(\Rightarrow\)∆ AOB = ∆ CHB (cạnh huyền, góc nhọn) ⇒ CH = AO ( 2 cạnh tương ứng )
A, O cố định ⇒ OA không đổi nên CH không đổi.
C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng OA.
Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.
Vậy C chuyển động trên tia Km // Ox, cách Ox một khoảng không đổi bằng OA.
Vì điểm C đối xứng với điểm A qua điểm B ⇒ BA = BC
Kẻ CH ⊥ Ox
Xét hai tam giác vuông AOB và CHB:
\(\widehat{AOB}=\widehat{CHB}=90^0\)
BA = BC (chứng minh trên)
\(\widehat{AOB}=\widehat{CBH}\)(đối đỉnh)
Do đó: ∆ AOB = ∆ CHB (cạnh huyền, góc nhọn) ⇒ CH = AO
A, O cố định ⇒ OA không đổi nên CH không đổi.
C thay đổi cách Ox một khoảng bằng OA không đổi nên C chuyển động trên đường thẳng song song với Ox, cách Ox một khoảng OA.
Khi B trùng O thì C trùng với điểm K đối xứng với A qua điểm O.
Vậy C chuyển động trên tia Km // Ox, cách Ox một khoảng không đổi bằng OA.