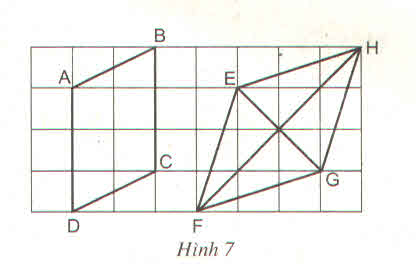
Các tứ giác ABCD, EFGH vẽ trên giấy kẻ ô vuông ở hình 7 có là hình bình hành không ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Cả ba tứ giác là hình bình hành
- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FG = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)
(Chú ý:
- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.
- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.)

Cả ba tứ giác là hình bình hành.
- Tứ giác ABCD là hình bình hành vì có
AB // CD và AB = CD =3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có
EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = QP và MQ = NP (dấu hiệu nhận biết 2)

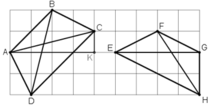
+ Xét tứ giác ABCD
Nhận thấy AB // CD ⇒ Tứ giác ABCD là hình thang.
Xét ΔACK vuông tại K ta có: AC2 = AK2 + KC2 = 42 + 12 = 17
Tương tự ta có BD2 = 42 + 12 = 17
⇒ AC2 = BD2
⇒ AC = BD
Vậy hình thang ABCD có hai đường chéo AC = BD nên là hình thang cân.
+ Xét tứ giác EFGH
FG // EH ⇒ Tứ giác EFGH là hình thang.
Lại có : EG = 4cm
FH2 = 22 + 32 = 13 ⇒ FH = √13 ≠ EG.
Vậy hình thang EFGH có hai đường chéo không bằng nhau nên không phải hình thang cân.

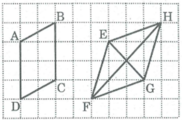
Tứ giác ABCD là hình bình hành vì có cạnh đối AD // BC và AD = BC bằng 3 cạnh ô vuông.
Tứ giác EFGH là hình bình hành vì có các cạnh đối bằng nhau.
EH = FG, EF = HG là đường chéo hình chữ nhật có cạnh 1 ô vuông và cạnh 3 ô vuông

Cắt hình theo mẫu rồi ghép thành hình bình hành hoặc hình tam giác