Cho hai đa thức \(A=2x^4-10x^3+3x^2-3x+2\)
\(B=2x^2+1\)
Tìm đa thức dư R trong phép chia A cho B rồi biết A = B.Q + R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 4 2019
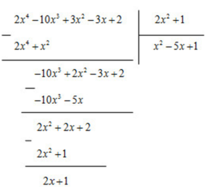
A = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1
Vậy đa thức dư R của phép chia A cho B là R = 2x + 1. Khi đó:
2 x 4 - 10 x 3 + 3 x 2 - 3 x + 2 = 2 x 2 + 1 x 2 - 5 x + 1 + 2 x + 1
LT
20 tháng 4 2017
Vậy 3x4 + x3 + 6x – 5 = (x2+ 1)(3x2 + x – 3) + 5x - 2
Xem thêm tại: http://loigiaihay.com/bai-69-trang-31-sgk-toan-8-tap-1-c43a4819.html#ixzz4entQxTTD
CM
29 tháng 11 2019
a) A = ( x 2 – 6x)B.
b) A = (-x – 8)B + 2
c) A = (x + 3)B + 6.
8 tháng 11 2021
Bài 1:
\(=\dfrac{x^3-x^2+x+3}{x+1}\)
\(=\dfrac{x^3+x^2-2x^2-2x+3x+3}{x+1}\)
\(=x^2-2x+3\)
CM
10 tháng 8 2018
Thực hiện phép chia ta có:
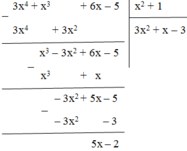
Vậy 3x4 + x3 + 6x – 5 = (x2 + 1).(3x2 + x – 3) + 5x – 2.
28 tháng 11 2018
Bài 1 :
Đặt tính chia như bình thường thôi bạn
Kết quả : ( 3x4 + x3 + 6x - 5 ) : ( x2 + 1 ) = 3x2 + x - 3 dư 5x - 2
Bài 2 :
Làm tương tự bài 1 ta có :
A : B = ( 2x3 - x2 - x + 1 ) : ( x2 - 2x ) = 2x + 3 dư 5x + 1
=> A = ( x2 - 2x ) . ( 2x + 3 ) + 5x + 1
\(\dfrac{A}{B}=\dfrac{2x^4-10x^3+3x^2-3x+2}{2x^2+1}=\dfrac{2x^4+x^2-10x^3-5x+2x^2+1+2x+1}{2x^2+1}\)
\(=x^2-x+1+\dfrac{2x+1}{2x^2+1}\)
R=2x+1
\(A=\left(x^2-x+1\right)\left(2x^2+1\right)+2x+1\)