Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc của tam giác đối diện với cạnh có độ dài 13 ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
14 tháng 10 2018
Ta có: 5 2 + 12 2 = 25 + 144 = 169 = 13 2
Vì tam giác có ba cạnh với độ dài các cạnh thỏa mãn định lí Pi-ta-go (bình phương một cạnh bằng tổng bình phương hai cạnh còn lại) nên nó là tam giác vuông.
Vậy góc đối diện với cạnh 13 (cạnh dài nhất) là góc vuông.
SC
25 tháng 3 2016
Gọi tam giác cần tìm là ABC có AB và AC là 2 cạnh góc vuông còn BC là cạnh huyền. Xét tam giác vuông ABC có : \(AB^2+AC^2=BC^2\)(định lí Py-ta-go) \(AB^2+AC^2=13^2=169\) Áp dụng tính chất dãy tỉ số bằng nhau ta có :\(\frac{AB^2}{12^2}=\frac{AC^2}{5^2}=\frac{AB^2+AC^2}{12^2+5^2}=\frac{169}{169}=1\) =>AB=144 AC=25
27 tháng 3 2020
sau khi tính ra AB=144 ; AC=25
thì phải tìm căn bậc 2 của nó
ĐÁp án đúng là AB=12; AC=5
KK
1
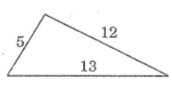
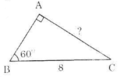
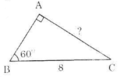
Vì \(5^5+12^2=169=13^2\) nên tam giác đã cho là tam giác vuông và góc đối diện với cạnh có độ dài 14 chính là góc vuông.