Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
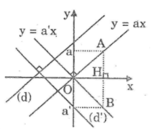
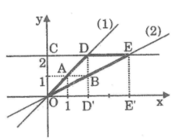
Qua gốc tọa độ, kẻ đường thẳng y = ax // (d) và y = a’x // (d’)
*Chứng minh (d) vuông góc với (d’) thì a.a’ = -1
Không mất tính tổng quát, giả sử a > 0
Khi đó góc tạo bởi tia Ox và đường thẳng y = ax là góc nhọn.
Suy ra góc tạo bởi tia Ox và đường thẳng y = a’x là góc tù (vì các góc tạo bởi đường thẳng y = ax và đường thẳng y = a’x với tia Ox hơn kém nhau 900).
Suy ra: a’ < 0
Mà đường thẳng y = ax đi qua A(1; a), đường thẳng y = a’x đi qua B(1; a’) nên đoạn AB vuông góc với Ox tại điểm H có hoành độ bằng 1.
Vì (d) ⊥ (d’) nên hai đường thẳng y = ax và y = a’x vuông góc với nhau. Suy ra: góc(AOB) = 90 °
Tam giác vuông AOB có OH ⊥ AB. Theo hệ thức lượng trong tam giác vuông, ta có: OH2 = HA.HB
Hay: a.|a’| = 1 ⇔ a.(-a’) = 1 ⇔ a.a’ = -1
Vậy nếu (d) vuông góc với (d’) thì a.a’ = -1
*Chứng minh a.a’ = -1 thì (d) vuông góc với (d’)
Ta có: a.a’ = -1 ⇔ a.|a’| = 1 hay HA.HB = O H 2
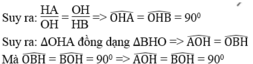
Suy ra OA ⊥ OB hay hai đường thẳng y = ax và y = a’x vuông góc với nhau hay (d) ⊥ (d’)
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
a: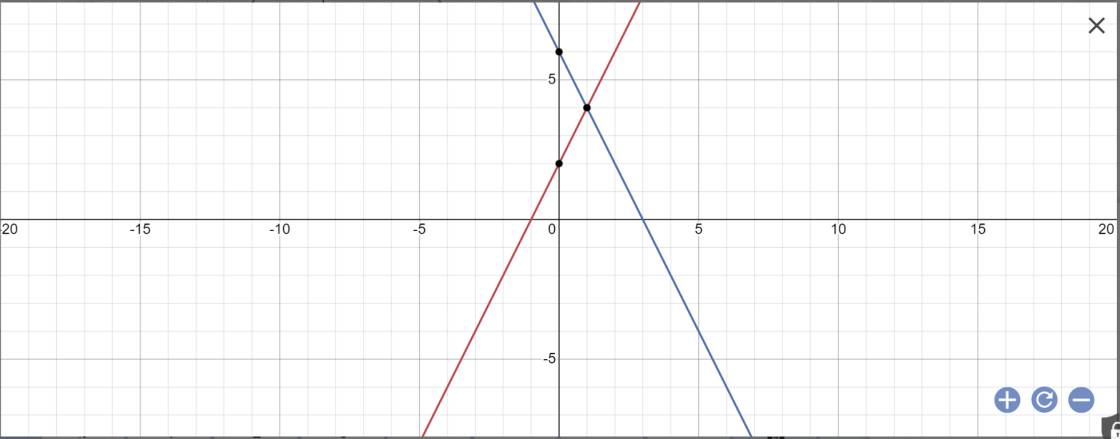 
b: Phương trình hoành độ giao điểm là:
2x+2=6-2x
=>2x+2x=6-2
=>4x=4
=>x=1
Thay x=1 vào y=2x+2, ta được:
\(y=2\cdot1+2=4\)
Vậy: (d1) cắt (d2) tại A(1;4)
c: Thay x=0 vào y=x-6, ta được:
y=0-6=-6
Thay x=0 và y=-6 vào y=ax+b, ta được:
\(a\cdot0+b=-6\)
=>b=-6
=>y=ax-6
Thay x=2 vào y=2x+1, ta được:
\(y=2\cdot2+1=5\)
Thay x=2 và y=5 vào y=ax-6, ta được:
2a-6=5
=>2a=11
=>\(a=\dfrac{11}{2}\)
a: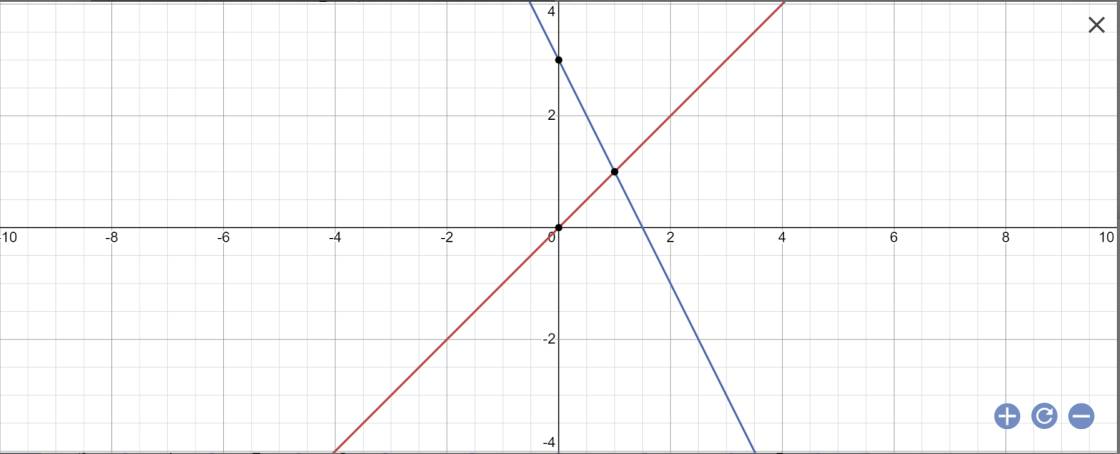 
b: (d1)//(d')
=>(d1): y=-2x+b
Thay x=0 và y=5 vào (d1), ta được:
b-2*0=5
=>b=5
c: Tọa độ giao điểm là;
x=-2x+3 và y=x
=>3x=3 và y=x
=>x=1 và y=1(ĐPCM)
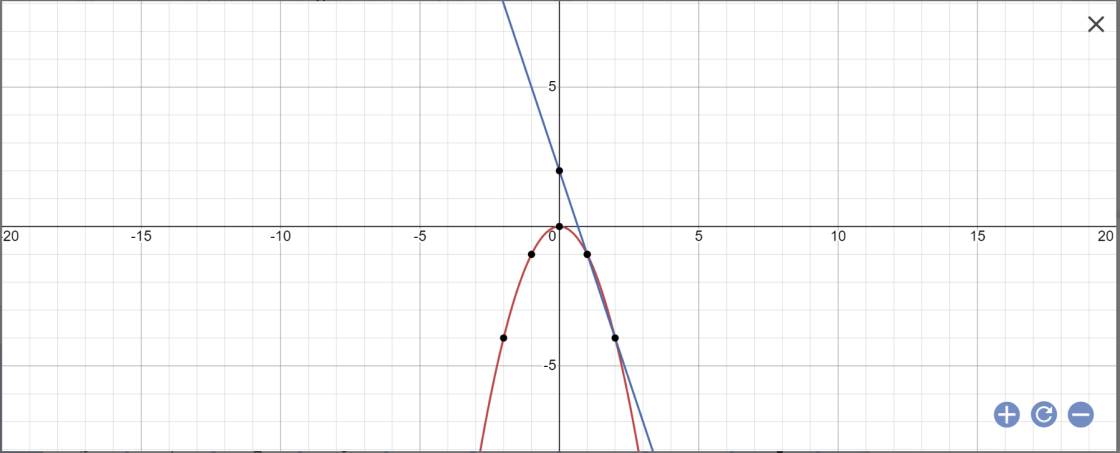
b) Phương trình hoành độ giao điểm của (P) và (d) là:
- x 2 = 2mx - 5 ⇔ x 2 + 2mx - 5 = 0
Δ'= m 2 + 5 > 0 với ∀m ∈ R
Vậy trên mặt phẳng Oxy đường thẳng (d) và Parabol (P) luôn cắt nhau tại hai điểm phân biệt.
Khi m = 2, phương trình hoành độ giao điểm của (P) và (d) là:
- x 2 = 4x - 5 ⇔ x 2 + 4x - 5 = 0
Δ = 4 2 - 4.1.(-5) = 36
⇒ Phương trình có 2 nghiệm
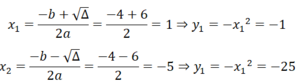
Vậy tọa độ hai giao điểm là M(1;-1) và N(-5;-25)
a: Thay x=1 vàp (P),ta được:
y=-1^2=-1
Thay x=2 vào (P), ta được:
y=-2^2=-4
Vì (d) đi qua A(1;-1) và B(2;-4) nên ta có hệ:
a+b=-1 và 2a+b=-4
=>a=-3 và b=2
c: (d): y=-3x+2 và (P): y=-x^2
