Tìm khoảng cách giữa hai điểm trên mặt phẳng tọa độ, biết rằng :
a) \(A\left(1;1\right)\) \(B\left(5;4\right)\)
b) \(M\left(-2;2\right)\) \(N\left(3;5\right)\)
c) \(P\left(x_1;y_1\right)\) \(Q\left(x_2;y_2\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
31 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
PT
1
CM
25 tháng 7 2017
Ta có: A B 2 = A C 2 + B C 2 = 5 - 1 2 + 4 - 1 2 = 16 + 9 = 25
AB = 25 = 5
PT
1
CM
13 tháng 10 2017
Ta có: M N 2 = M D 2 + N D 2 = 3 + 2 2 + 3 - 2 2 = 25 + 9 = 34
AB = 34 ≈ 5,83
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
\(AB=\sqrt{\left(5-\left(-3\right)\right)^2+\left(5-1\right)^2}=\sqrt{8^2+4^2}=4\sqrt{5}\)
CM
24 tháng 7 2018
Đáp án D
Phương pháp :
Gọi (Q): x+y+z+a=0 a ≠ 0 là mặt phẳng song song với mặt phẳng (P).
Sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.
Cách giải :
Gọi (Q): x+y+z+a=0 a ≠ 0 là mặt phẳng song song với mặt phẳng (P).
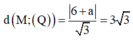
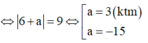
Vậy không có mặt phẳng (Q) nào thỏa mãn điều kiện bài toán.
19 tháng 3 2016
a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .