Chứng minh các định lí sau :
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
24 tháng 3 2019
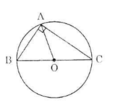
Hình a) + b)
a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.
Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.
=> O là tâm của đường tròn đi qua A, B, C.
Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:
OA = OB = OC
Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)
CM
19 tháng 10 2017
a, Giả sử ∆ABC vuông tại A. Gọi O là trung điểm của BC
=> OA = OB = OC => O là tâm đường tròn đi qua A,B,C
b, Ta có OA = OB = OC => OA = 1 2 BC => ∆ABC vuông tại A
22 tháng 3 2016
a) Xét tam giác ABC vuông tại A.
Gọi O là trung điểm của cạnh huyền BC, ta có:
OA=OB=OC.
Vậy O chính là tâm cuả đường tròn ngoại tiếp tam giác ABC
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC.
Ta có OA=OB=OC(=R)
suy ra OA = 1/2BC , do đó tam giác ABC vuông tại A
Nhận xét: Định lý trong bài tập này thường được dùng để giải nhiều bài tập về nhận biết tam giác vuông.
CM
10 tháng 5 2017
Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:
OA = OB = OC
Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC nên suy ra tam giác ABC vuông tại A. (đpcm)
CM
6 tháng 4 2017
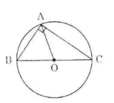
Hình a) + b)
a) Xét tam giác ABC vuông tại A. Gọi O là trung điểm của BC.
Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.
=> O là tâm của đường tròn đi qua A, B, C.
Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)
a) Xét tam giác ABC vuông tại A.
Gọi O là trung điểm của cạnh huyền BC, ta có:
OA=OB=OC.
Vậy O chính là tâm cuả đường tròn ngoại tiếp tam giác ABC
b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC.
Ta có OA=OB=OC(=R)
suy ra OA=12BC, do đó tam giác ABC vuông tại A
Nhận xét: Định lý trong bài tập này thường được dùng để giải nhiều bài tập về nhận biết tam giác vuông.