Tìm tam giác bằng nhau trên hình 148 :
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
17 tháng 5 2018
+ Hai tam giác vuông AMD và AME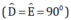 
có:
AM chung
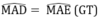
⇒ ΔAMD = ΔAME ( cạnh huyền - góc nhọn)
⇒ MD = ME và AD = AE ( Hai cạnh tương ứng) (1)
+ Hai tam giác vuông MDB và MEC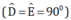 
có
MB = MC (GT)
MD = ME (chứng minh trên)
⇒ ΔMDB = ΔMEC ( cạnh huyền – cạnh góc vuông)
⇒ BD=CE ( hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD+BD=AE+CE ⇒ AB=AC.
+ Xét ΔAMB và ΔAMC có:
MB = MC (GT)
AB = AC (chứng minh trên)
AM chung
⇒ ΔAMB = ΔAMC (c.c.c)
TA
11 tháng 2 2021
Với đề bài đã cho , đặt chiều rộng HCN là a , chiều dài là b , cạnh tam giác là c , cạnh hình vuông là d , diện tích là S , chu vi là C .
Ta có các ĐK :
( a + b ) x 2 = C ; c x 3 = C ; d x 4 = C ; a x b + d x d = 425cm2
=> a + a x 2 = C/2 ; c = C/3 ; d = C/4
=> a + a + a = C/2 ; c = C/3 ; d = C/4
=> a = C/6 ; c = C/3 ; d = C/4
=> a x 6 = C ; c = C/3 ; d = C/4
=> a = 3 ; b = 6 <=> C = 18 => c = 6 ; d = 4,25
Quay trở lại với ĐK : a x b + d x d = 425cm2 , ta có :
a x b + d x d = 425cm2
a x a x 2 + d x d = 425cm2
3 x 3 x 2 + 4,25 x 4,25 = 425cm2
18 + 18,0625 = 425cm2
Sai thì nhắn tin với mình nhé , không đúng đâu , mình chỉ biết vậy thôi.
1 tháng 1 2022
Trước hết ta cần chứng minh bổ đề sau (tạm gọi là bổ đề 1): Nếu 2 tam giác mà có chung đường cao tương ứng ( hay 2 đường cao tương ứng bằng nhau) thì tỉ số diện tích của hai tam giác bằng tỉ số cạnh đáy tương ứng.
Hạ đường cao chung AH của hai tam giác ABM và ACM. Ta cần chứng minh \(\frac{S_{ABM}}{S_{ACM}}=\frac{BM}{CM}\)
Thật vậy: \(S_{ABM}=\frac{1}{2}AH.BM\); \(S_{ACM}=\frac{1}{2}AH.CM\)
\(\Rightarrow\frac{S_{ABM}}{S_{ACM}}=\frac{\frac{1}{2}AH.BM}{\frac{1}{2}AH.CM}=\frac{BM}{CM}\)
Như vậy bổ đề được chứng minh.
1 tháng 1 2022
Một sự thật nghiệt ngã đó là muốn MN chia tam giác ABC thành 2 phần có diện tích bằng nhau thì chỉ còn nước M trùng với B mà thôi.
Muốn MN chia tam giác ABC thành 2 phần có dt bằng nhau thì điều hiển nhiên là \(\frac{S_{CMN}}{S_{ABC}}=\frac{1}{2}\)(dt tam giác CMN bằng một nửa dt tam giác ABC)
Giả sử M nằm trên cạnh BC nhưng M không trùng với B, ta sẽ có \(CM< BC\)\(\Leftrightarrow\frac{CM}{BC}< 1\)
Hai tam giác CMN và BCN có chung đường cao hạ từ N nên \(\frac{S_{CMN}}{S_{BCN}}=\frac{CM}{BC}\)(hai tam giác có chung đường cao thì tỉ số diện tích bằng tỉ số hai cạnh đáy tương ứng)
Từ đó ta có \(\frac{S_{CMN}}{S_{BCN}}< 1\)(1)
Mặt khác hai tam giác BCN và ABC có chung đường cao hạ từ B nên \(\frac{S_{BCN}}{S_{ABC}}=\frac{NC}{AC}\)
Do N nằm trên AC sao cho \(NA=NC\)nên \(\frac{NC}{AC}=\frac{1}{2}\)(NC bằng một nửa AC)
Từ đó \(\frac{S_{BCN}}{S_{ABC}}=\frac{1}{2}\)(2)
Nhân vế theo vế của (1) và (2), ta có: \(\frac{S_{CMN}}{S_{BCN}}.\frac{S_{BCN}}{S_{ABC}}< 1.\frac{1}{2}\)\(\Leftrightarrow\frac{S_{CMN}}{S_{ABC}}< \frac{1}{2}\)
Như vậy rõ ràng khi N không trùng với B thì việc MN chia tam giác ABC thành 2 phần có dt bằng nhau là không thể.
Do đó N trùng với B.
CM
9 tháng 1 2018
Gọi độ dài cạnh tam giác và cạnh tứ giác là a,b (cm) (a > b)
Cạnh của tam giác dài hơn cạnh của tứ giác là 10cm nên:
a – b = 10 cm => a = 10 + b
Chu vi tam giác bằng chu vi tứ giác nên:
a + a + a = 4 × b => 3 × a = 4 × b => 3 × (10 + b) = 4 × b => 30 + 3 × b = 4 × b => b = 30 cm
Suy ra a = 10 + 30 = 40 cm
Vậy độ dài cạnh tam giác là 40 cm và độ dài cạnh tứ giác là 30cm
26 tháng 5 2017
C là chu vi
C_ABC = C_MNPQ
Mà ABC chỉ có 3 cạnh, còn MNPQ có 4 cạnh.
Mặt khác, cạnh tam giác ABC lớn hơn cạnh tứ giác MNPQ 10cm. Vậy , mỗi cạnh của tam giác ABC phải "bù" cho cạnh tứ giác MNPQ 10cm.
Độ dài mỗi cạnh của tứ giác MNPQ : 10 * 3 = 30(cm)
Độ dài mỗi cạnh của tam giác ABC : 10 * 4 = 40 (cm) hoặc 30 + 10 = 40 (cm)
26 tháng 5 2017
c là chu vi của hình tam giác
c- abc=c-mnpq
mà hình tam giác abc chỉ có 3 cánh còn mnpq có tới 4 cạnh
cạnh tam giác lớn hơn cạnh hình tứ giác là 10 cm suy ra mỗi cạnh của tam giác phải đưa cho cạnh tứ giác kia 10 cm
Ta có: ∆AMD=∆AME(Cạnh huyền AM chung, góc nhọn^A1 = ^A2)
∆MDB=∆MEC(Cạnh huyền BM=CM, cạnh góc vuông.
MD=ME, do ∆AMD=∆AME)
∆AMB= ∆AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC
Ta có: \(\Delta\)AMD=\(\Delta\)AME(Cạnh huyền AM chung, góc nhọn \(\widehat{A}_1=\widehat{A}_2\))
\(\Delta\)MDB=\(\Delta\)MEC(Cạnh huyền BM=CM, cạnh góc vuông )
MD=ME, do \(\Delta\)AMD=\(\Delta\)AME)
\(\Delta\)AMB= \(\Delta\)AMC(Cạnh AM chung),
Cạnh MB=MC, cạnh AB=AC
Vì AD=AE, DB=EC