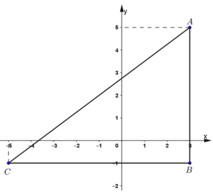
Trong mặt phẳng tọa độ vẽ tam giác ABC với các đỉnh \(A\left(3;5\right);B\left(3;-1\right);C\left(-5;-1\right)\). Tam giác ABC là tam giác gì ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
BK
2
Tam giác ABC là tam giác vuông tại B. 
12 tháng 12 2020
chuẩn rồi bạn là người đẹp trai và học giỏi nhất thế giới
BẠN RẤT ĐẸP TROAI
BT
18 tháng 5 2017
a)Gọi \(D\left(x;y\right)\) là tọa độ điểm cần tìm.
\(\overrightarrow{AD}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
Tứ giác ABCD là hình bình hành khi và chỉ khi:
\(\overrightarrow{AD}=\overrightarrow{BC}\)\(\Leftrightarrow\left\{{}\begin{matrix}x-2=2\\y-4=-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)\(\Rightarrow D\left(4;0\right)\).
b) Gọi\(A'\left(x;y\right)\) là điểm cần tìm. A' thỏa mãn hai điều sau:
- \(AA'\perp BC\). (1)
- A' , B, C thẳng hàng. (2)
\(\overrightarrow{AA'}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
\(\left(1\right)\Leftrightarrow\overrightarrow{AA'}.\overrightarrow{BC}=\overrightarrow{0}\)\(\Leftrightarrow2\left(x-2\right)-4\left(y-4\right)=0\) (3)
(2) suy ra hai véc tơ \(\overrightarrow{A'B}\) và \(\overrightarrow{BC}\) cùng phương.
Có \(\overrightarrow{A'B}\left(1-x;3-y\right)\).
Nên \(\dfrac{1-x}{2}=\dfrac{3-y}{4}\) (4)
Từ (3) và (4) suy ra: \(\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\).
Vậy A'(1;3).
13 tháng 10 2017
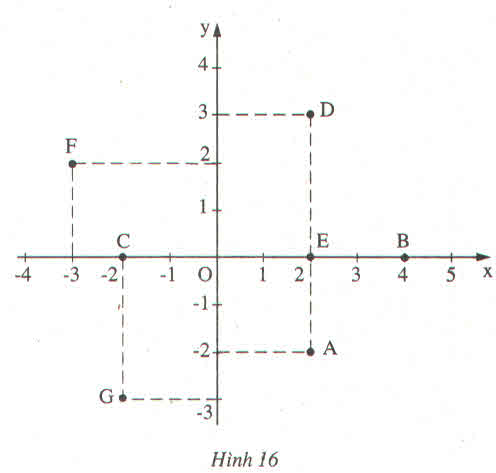
a) Tọa độ các điểm trong hình vẽ là:
A(2;-2); B(4;0); C(-2;0); D(2;3); E(2;0);F(-3;2); G(-2;-3)
b) Ta có hình vẽ ∆ABC:
A(-3;4); B(-3;1); C(1;-1).
NV
Nguyễn Việt Lâm
Giáo viên
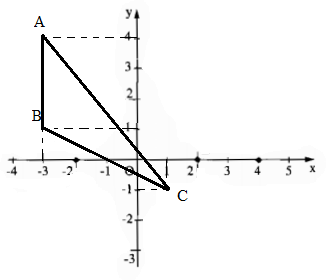
21 tháng 3 2021
Bạn coi lại đề, 2 đường thẳng xuất phát từ B nhưng lại song song với nhau, điều này hoàn toàn vô lý
Tam giác ABC là tam giác vuông tại B.
Tam giác ABC là tam giác vuông tại B