Câu 1
a) Tính \(2\sqrt{6}-\sqrt{49}\)
b) CMR \(\dfrac{1}{3+\sqrt{2}}+\dfrac{1}{3-\sqrt{2}}=\dfrac{6}{7}\)
c) Rút gọn biểu thức \(B=\left(1+\dfrac{a+\sqrt{a}}{\sqrt{a}+1}\right)\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)với...a\ge0;a\ne1\)
Câu 2Cho phương trình \(x^2-2\left(m-3\right)x-1=0\)
Tìm m để phương trình có nghiệm \(x_1;x_2\)mà biểu thức \(A=x^2_1-x_1x_2+x^2_2\)đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right)\cdot\dfrac{x-4}{3\sqrt{x}}\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{x-4}{3\sqrt{x}}\)
\(=\dfrac{2}{3}\)

1. ĐKXĐ: $x>0; x\neq 9$
\(A=\frac{\sqrt{x}+3+\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{\sqrt{x}}=\frac{2\sqrt{x}}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{\sqrt{x}}=\frac{2}{\sqrt{x}+3}\)
2. ĐKXĐ: $x\geq 0; x\neq 4$
\(B=\left[\frac{\sqrt{x}(\sqrt{x}+2)+\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)}+\frac{6-7\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}\right](\sqrt{x}+2)\)
\(=\frac{x+3\sqrt{x}-2+6-7\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.(\sqrt{x}+2)=\frac{x-4\sqrt{x}+4}{\sqrt{x}-2}=\frac{(\sqrt{x}-2)^2}{\sqrt{x}-2}=\sqrt{x}-2\)

\(a,=\dfrac{\sqrt{5}+1+\sqrt{5}-1}{\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)}=\dfrac{2\sqrt{5}}{4}=\dfrac{\sqrt{5}}{2}\\ b,=\sqrt{\left(3-\sqrt{5}\right)^2}+\left|2-\sqrt{5}\right|=3-\sqrt{5}+\sqrt{5}-2=1\\ c,=\dfrac{2\left(\sqrt{5}-\sqrt{3}\right)}{2}-\dfrac{-\sqrt{3}\left(\sqrt{5}-\sqrt{3}\right)}{\sqrt{5}-\sqrt{3}}=\sqrt{5}-\sqrt{3}+\sqrt{3}=\sqrt{5}\)

\(A=\dfrac{2-\sqrt{a}-\sqrt{a}-3}{2\sqrt{a}+1}=-1\)
\(B=\dfrac{1}{1-\sqrt{2+\sqrt{3}}}-\dfrac{1}{1-\sqrt{2-\sqrt{3}}}\)
\(=\dfrac{\sqrt{2}}{\sqrt{2}-\sqrt{3}-1}-\dfrac{\sqrt{2}}{\sqrt{2}-\sqrt{3}+1}\)
\(=\dfrac{2-\sqrt{6}+\sqrt{2}-2+\sqrt{6}+\sqrt{2}}{5-2\sqrt{6}-1}\)
\(=\dfrac{2\sqrt{2}}{4-2\sqrt{6}}=\dfrac{1}{\sqrt{2}-\sqrt{3}}=-\sqrt{2}-\sqrt{3}\)

a) \(A=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right).\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\left(đk:a>0,x\ne1\right)\)
\(=\dfrac{a-1}{2\sqrt{a}}.\dfrac{\left(a-\sqrt{a}\right)\left(\sqrt{a}-1\right)-\left(a+\sqrt{a}\right)\left(\sqrt{a}+1\right)}{a-1}\)
\(=\dfrac{a\sqrt{a}-2a+\sqrt{a}-a\sqrt{a}-2a-\sqrt{a}}{2\sqrt{a}}\)
\(=\dfrac{-4a}{2\sqrt{a}}=-2\sqrt{a}\)
b) \(A=-2\sqrt{a}>-6\)
\(\Leftrightarrow\sqrt{a}< 3\Leftrightarrow0\le a< 9\) và \(a\ne1\)
c) \(a^2-3=0\Leftrightarrow a^2=3\Leftrightarrow\sqrt{a}=\sqrt[4]{3}\)
\(\Rightarrow A=-2\sqrt{a}=-2\sqrt[4]{3}\)

1:
\(A=\sqrt{x^2+\dfrac{2x^2}{3}}=\sqrt{\dfrac{5x^2}{3}}=\left|\sqrt{\dfrac{5}{3}}x\right|=-x\sqrt{\dfrac{5}{3}}\)
2: \(=\left(\dfrac{\sqrt{100}+\sqrt{40}}{\sqrt{5}+\sqrt{2}}+\sqrt{6}\right)\cdot\dfrac{2\sqrt{5}-\sqrt{6}}{2}\)
\(=\dfrac{\left(2\sqrt{5}+\sqrt{6}\right)\left(2\sqrt{5}-\sqrt{6}\right)}{2}\)
\(=\dfrac{20-6}{2}=7\)

a) Ta có: \(A=\left(\dfrac{1}{\sqrt{a}+2}+\dfrac{1}{\sqrt{a}-2}\right):\dfrac{\sqrt{a}}{a-4}\)
\(=\dfrac{\sqrt{a}-2+\sqrt{a}+2}{\left(\sqrt{a}-2\right)\left(\sqrt{a}+2\right)}\cdot\dfrac{\left(\sqrt{a}+2\right)\left(\sqrt{a}-2\right)}{\sqrt{a}}\)
=2
b) Ta có: \(B=\left(\dfrac{4x}{\sqrt{x}-1}-\dfrac{\sqrt{x}-2}{x-3\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}-1}{x^2}\)
\(=\dfrac{4x-1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}-1}{x^2}\)
\(=\dfrac{4x-1}{x^2}\)

a ĐKXĐ \(a\ge0,a\ne\dfrac{1}{4},a\ne1\)
\(\Rightarrow P=1+\left(\dfrac{\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}\right)}-\dfrac{\sqrt{a}\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)}\right)\cdot\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{2\sqrt{a}-1}\)
= \(1+\left(\dfrac{\left(-1\right)\left(2\sqrt{a}-1\right)}{\sqrt{a}-1}+\dfrac{\sqrt{a}\left(2\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)}\right)\cdot\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{2\sqrt{a}-1}\)
= \(1+\left(-1+\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{a+\sqrt{a}+1}\right)\sqrt{a}\)
= \(1-\sqrt{a}+\dfrac{a\sqrt{a}+a}{a+\sqrt{a}+1}\) = \(\dfrac{\left(1-\sqrt{a}\right)\left(1+\sqrt{a}+a\right)+a\sqrt{a}+a}{a+\sqrt{a}+1}=\dfrac{1-a\sqrt{a}+a\sqrt{a}+a}{a+\sqrt{a}+1}=\dfrac{a+1}{a+\sqrt{a}+1}\)
b Xét hiệu \(P-\dfrac{2}{3}=\dfrac{a+1}{a+\sqrt{a}+1}-\dfrac{2}{3}=\dfrac{3a+3-2a-2\sqrt{a}-2}{a+\sqrt{a}+1}=\dfrac{a-2\sqrt{a}+1}{a+\sqrt{a}+1}=\dfrac{\left(\sqrt{a}-1\right)^2}{a+\sqrt{a}+\dfrac{1}{4}+\dfrac{3}{4}}=\dfrac{\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}+\dfrac{1}{2}\right)^2+\dfrac{3}{4}}>0\) \(\Rightarrow P>\dfrac{2}{3}\)
c Ta có \(P=\dfrac{\sqrt{6}}{\sqrt{6}+1}\Rightarrow\dfrac{a+1}{a+\sqrt{a}+1}=\dfrac{\sqrt{6}}{\sqrt{6}+1}\) \(\Rightarrow\left(a+1\right)\left(\sqrt{6}+1\right)=\sqrt{6}\left(a+\sqrt{a}+1\right)\Leftrightarrow a\sqrt{6}+a+\sqrt{6}+1=a\sqrt{6}+\sqrt{6a}+\sqrt{6}\)
\(\Leftrightarrow a-\sqrt{6a}+1=0\Leftrightarrow a-\sqrt{6a}+\dfrac{6}{4}-\dfrac{2}{4}=0\Leftrightarrow\left(\sqrt{a}-\dfrac{\sqrt{6}}{2}\right)^2=\dfrac{1}{2}\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{a}=\dfrac{\sqrt{6}+1}{2}\\\sqrt{a}=\dfrac{1-\sqrt{6}}{2}\left(L\right)\end{matrix}\right.\) (Do \(\sqrt{a}\ge0\)) \(\Rightarrow a=\dfrac{\left(\sqrt{6}+1\right)^2}{4}=\dfrac{7+2\sqrt{6}}{4}\left(TM\right)\)
Vậy...
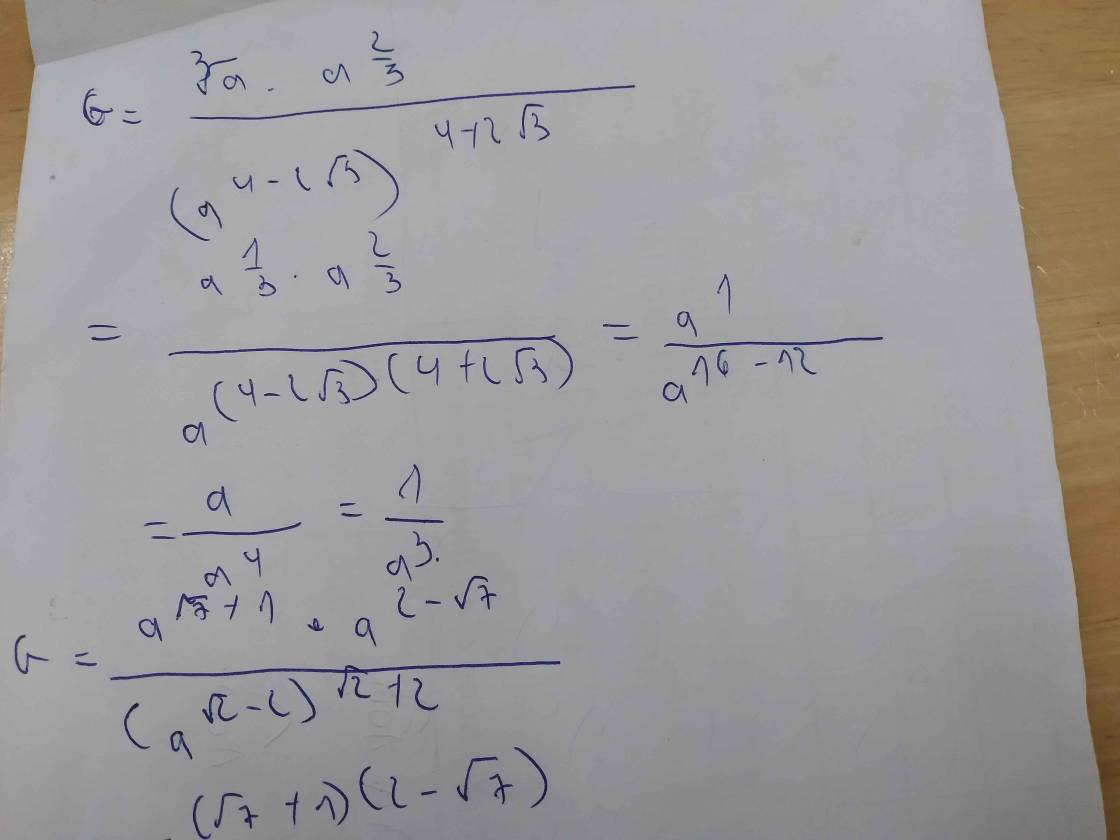

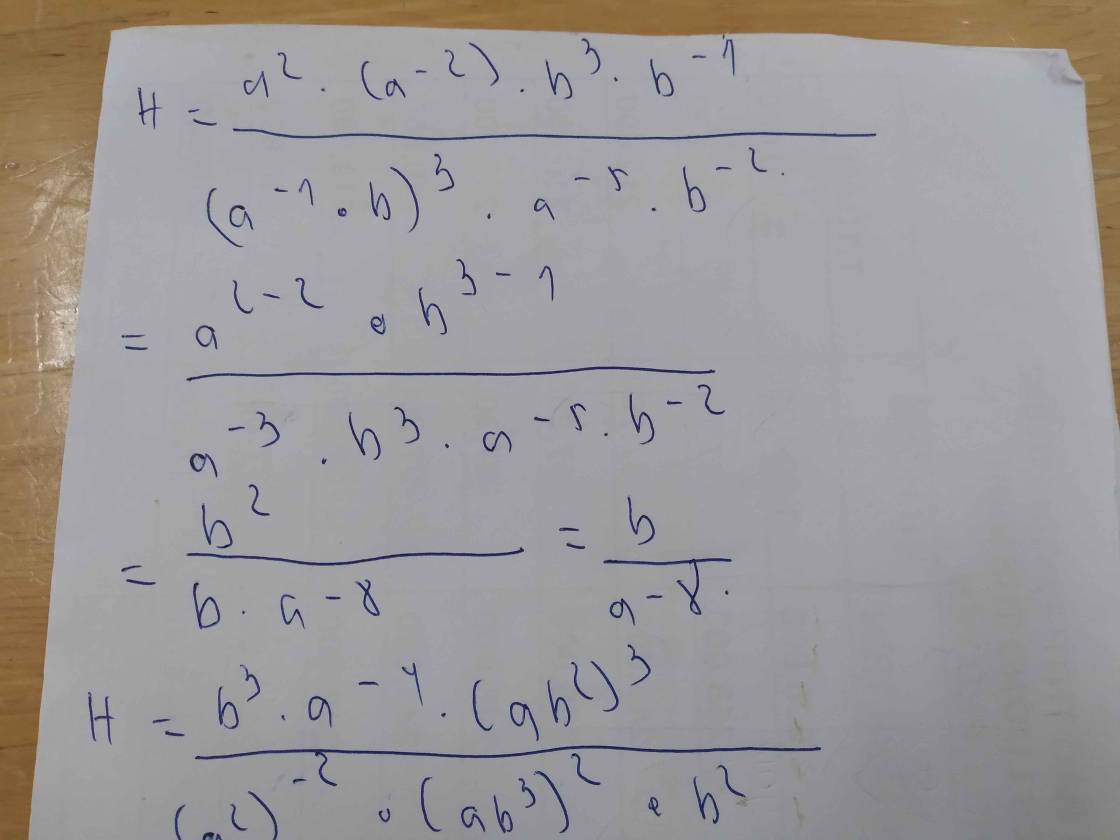
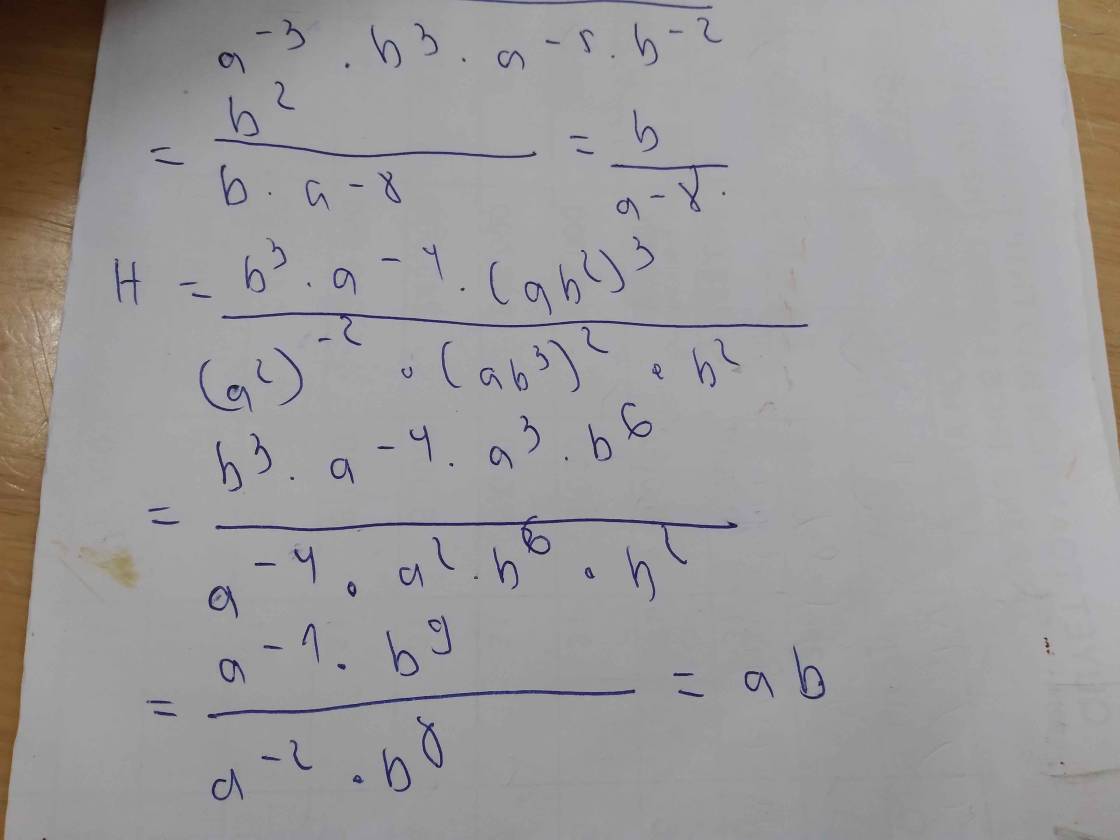

Câu 2:
\(x^2-2\left(m-3\right)x-1=0\)
a=1; b=-2m+6; c=-1
Vì ac<0 nên phương trình luôn có hai nghiệm phân biệt
Ta có: \(A=x_1^2+x_2^2-x_1x_2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\)
\(=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=\left(2m-6\right)^2-3\cdot\left(-1\right)\)
\(=4m^2-24m+36+3\)
\(=\left(2m-6\right)^2+3\ge3\)
Dấu '=' xảy ra khi m=3