Trên mặt phẳng Oxy, tìm tập hợp điểm biểu diễn các số phức \(z\) thỏa mãn điều kiện \(\left|z-i\right|=\left|\left(1+i\right)z\right|\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
5 tháng 7 2017
Giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực
Ta có:
\(|z-3+4i|=2\Leftrightarrow |(a-3)+i(b+4)|=2\)
\(\Leftrightarrow (a-3)^2+(b+4)^2=4\)
Vậy tập hợp các điểm biểu diễn số phức $z$ nằm trên đường tròn tâm \((3;-4)\) bán kính \(R=2\)
1 tháng 4 2017
Giả sử z = x + yi, (x,y ε R), khi đó trên mặt phẳng toạ độ Oxy, điểm M(x;y) biểu diễn số phức z.
a) Ta có |z| = 1 ⇔ 
= 1 ⇔ x2 + y2 = 1.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tam O, bán kính bằng 1
b) Ta có |z| ≤ 1 ⇔ ≤ 1 ⇔ x2 + y2 ≤ 1.
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 1 (kể cả các điểm trên đường tròn) (hình b)
c) Ta có 1 < |z| ≤ 2 ⇔ 1 < ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm O, bán kính bằng 1 (không kể điểm trên đường tròn này) và đường tròn tâm O, bán kính bằng 2 (kể cả các điểm trên đường tròn này)
d) Ta có |z| = 1 ⇔ = 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1. Suy ra x = 0 và y = 1
Vậy tập hợp các điểm cần tìm là điểm A(0;1)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 4 2021
\(\Leftrightarrow\left(1-2i\right)z-\left(\dfrac{1}{2}-\dfrac{3}{2}i\right)=\left(3-i\right)z\)
\(\Leftrightarrow\left(1-2i\right)z-\left(3-i\right)z=\dfrac{1}{2}-\dfrac{3}{2}i\)
\(\Leftrightarrow\left(-2-i\right)z=\dfrac{1}{2}-\dfrac{3}{2}i\)
\(\Rightarrow z=\dfrac{1-3i}{2\left(-2-i\right)}=\dfrac{1}{10}+\dfrac{7}{10}i\)
\(\Rightarrow A\left(\dfrac{1}{10};\dfrac{7}{10}\right)\) \(\Rightarrow\) tọa độ trung điểm I là \(\left(\dfrac{1}{20};\dfrac{7}{20}\right)\)
CM
6 tháng 9 2018
Đặt z = x + yi. Từ |z – i| = |(1 + i)z| suy ra :
x 2 + ( y + 1 ) 2 = 2
Các điểm biểu diễn z nằm trên đường tròn tâm I(0; -1) bán kính
CM
15 tháng 8 2019
Đặt z = x + yi. Từ |z – i| = |(1 + i)z| suy ra :
x 2 + y + 1 2 = 2
Các điểm biểu diễn z nằm trên đường tròn tâm I(0; -1) bán kính
CM
25 tháng 1 2017
Gọi z = a + bi với a , b ∈ R
Ta có 1 ≤ z - 2 i < 2 ⇔ 1 ≤ a 2 + b - 2 2 < 4
Vậy tập hợp các điểm M là hình tròn tâm I ( 0;2 ) và bán kính R = 2 đồng thời trừ đi hình tròn tâm I ( 0;2 ) bán kính R' = 1 . (Chúng ta thường nhầm lẫn giữa hai đáp án C và D )
Đáp án D
CM
21 tháng 9 2019
Chọn D.
Gọi M(x; y) là điểm biểu diễn số phức z = x + yi, x, y ∈ R
Gọi A là điểm biểu diễn số phức 2
Gọi B là điểm biểu diễn số phức -2
Ta có: |z – 2| + |z + 2| = 10 ⇔ MB + MA = 10.
Ta có AB = 4.
Suy ra tập hợp điểm M biểu diễn số phức z là Elip với 2 tiêu điểm là A(2; 0), B( -2; 0) tiêu cự AB = 4 = 2c, độ dài trục lớn là 10 = 2a , độ dài trục bé là 
Vậy tập hợp các điểm biểu diễn các số phức z thỏa mãn điều kiện |z – 2| + |z + 2| = 10 là elip có phương trình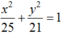 
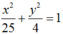
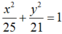
Giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực
Ta có:
\(|z-i|=|(1+i)z|\Leftrightarrow |a+i(b-1)|=|z||1+i|=|a+bi|\sqrt{2}\)
\(\Leftrightarrow a^2+(b-1)^2=2(a^2+b^2)\)
\(\Leftrightarrow a^2+(b+1)^2=2\)
Vậy tập hợp biểu diễn số phức $z$ nằm trên đường tròn tâm \((0,-1)\) bán kính \(R=\sqrt{2}\)