a) Cho số phức z. Chứng minh rằng z là một số thực khi và chỉ khi \(z=\overline{z}\)
b) Chứng tỏ rằng số phúc sau là một số thực :
\(z=-\dfrac{3+2i\sqrt{3}}{\sqrt{2}+3i}+\dfrac{-3+2i\sqrt{3}}{\sqrt{2}-3i}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B.
Ta có: Phần thực: –4, phần ảo: –3
![]()
Hai ý (3) và (4) sai.

Hiển nhiên nếu z
∈
R, z
≠
−1 thì 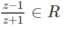
Ngược lại, nếu 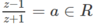
thì z – 1 = az + a và a ≠ 1
Suy ra (1 − a)z = a + 1
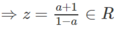
và hiển nhiên z ≠ −1.

Hiển nhiên nếu \(z\in\mathbb{R},z\ne-1\) thì \(\dfrac{z-1}{z+1}\in\mathbb{R}\)
Ngược lại, nếu \(\dfrac{z-1}{z+1}=a\in\mathbb{R}\) thì \(z-1=az+a\) và \(a\ne1\)
Suy ra \(\left(1-a\right)z=a+1\Rightarrow\)\(z=\dfrac{a+1}{1-a}\in\mathbb{R}\) và hiển nhiên \(z\ne-1\)

Hiển nhiên nếu z ∈ R, z ≠ −1 thì 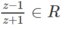
Ngược lại, nếu 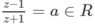
thì z – 1 = az + a và a ≠ 1
Suy ra (1 − a)z = a + 1
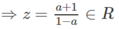
và hiển nhiên z ≠ −1.