Cho tam giác ABC biết \(a=14cm,b=18cm,c=20cm\). Tính \(\widehat{A};\widehat{B};\widehat{C}\) ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình bạn tự vẽ ạ.
a, Xét \(\Delta ADE\) và \(\Delta ABC\) có :
\(\dfrac{AD}{AB}=\dfrac{7}{14}=\dfrac{1}{2}\)
\(\dfrac{AE}{AC}=\dfrac{10}{20}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(=\dfrac{1}{2}\right)\)
Mà \(\widehat{A}:chung\)
\(\Rightarrow\Delta ADE\sim\Delta ABC\left(c-g-c\right)\)
b, Ta có : \(\Delta ADE\sim\Delta ABC\left(cmt\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{ED}{BC}\)
hay \(\dfrac{7}{14}=\dfrac{ED}{18}\)
\(\Rightarrow ED=\dfrac{7.18}{14}=9\left(cm\right)\)

a) (H.a)
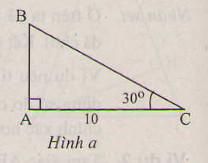
ˆB=90∘−30∘=60∘.B^=90∘−30∘=60∘.
AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)AB=AC⋅tgC=10⋅tg30∘≈5,774(cm)
BC=ACcosC=10cos30∘≈11,547(cm)BC=ACcosC=10cos30∘≈11,547(cm).
b) (H.b)
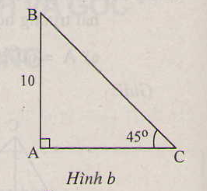
ˆB=90∘−45∘=45∘.B^=90∘−45∘=45∘.
⇒AC=AB=10(cm);⇒AC=AB=10(cm);
BC=ABsinC=10sin45∘≈14,142(cm)BC=ABsinC=10sin45∘≈14,142(cm)
c) (H.c)
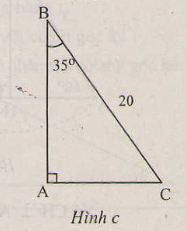
ˆC=90∘−35

Do tam giác ABC cân AB =4cm, AC = 8cm => BC = 8cm
Chu vi tam giác sẽ là: 4 +8 +8 = 20cm
Đáp án C
Các bạn muốn giải đáp thắc mắc hoặc kèm thêm toán thì có thể liên hệ nhé
Do tam giác ABC cân AB =4cm, AC = 8cm => BC = 8cm
Chu vi tam giác sẽ là: 4 +8 +8 = 20cm

a,chu vi của hình tam giác là :
15 + 20 + 25 = 60 ( cm )
đáp số : 60 cm
b, chu vi của hình tứ giác là :
12 + 14 + 16 + 18 = 60 ( cm )
đáp số : 60 cm
a) Chu vi của tam giác đó là
15+20+25=60 (cm)
Đáp số: 60 cm
b) Chu vi của tứ giác đó là
12+14+16+18=60 (cm)
Đáp số: 60cm

(Lưu ý: ΔABC vuông tại A nên ∠ B + ∠ C = 90 °
Giải tam giác tức là đi tìm số đo các cạnh và các góc còn lại.)
a)
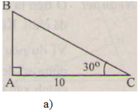
∠ B = 90 o - ∠ C = 90 ° - 30 ° = 60 °
c = b . t g C = 10 . t g 30 ° ≈ 5 , 77 ( c m )
![]()
b)
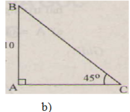
∠ B = 90 ° - ∠ C = 90 ° - 45 ° = 45 °
=> ΔABC cân => b = c = 10 (cm)
![]()
c)
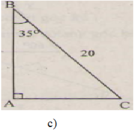
∠ B = 90 o - ∠ C = 90 ° - 35 ° = 55 ° b = a sin B = 20 . sin 35 ° ≈ 11 , 47 ( c m ) c = a sin C = 20 . sin 55 ° ≈ 16 , 38 ( c m )
d)
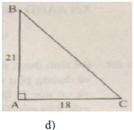
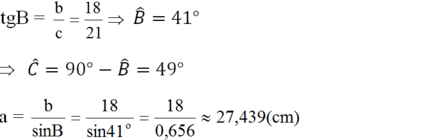
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(\Leftrightarrow AB=10\cdot\dfrac{\sqrt{3}}{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=10^2+\left(\dfrac{10\sqrt{3}}{3}\right)^2=\dfrac{400}{3}\)
hay \(BC=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{C}=50^0\)
Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin\widehat{C}\)
\(\Leftrightarrow AB=20\cdot\sin50^0\)
hay \(AB\simeq15,32\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=20^2-15.32^2=165.2976\)
hay \(AC\simeq12,86\left(cm\right)\)
\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{18^2+20^2-14^2}{2.18.20}=\dfrac{11}{15}\).
Vậy \(\widehat{A}=42^o50'\).
\(cosB=\dfrac{a^2+c^2-b^2}{2ac}=\dfrac{14^2+20^2-18^2}{2.14.20}=\dfrac{17}{20}\).
Vậy \(\widehat{B}=60^o56'\).
Vậy \(\widehat{C}=180^o-\widehat{A}-\widehat{B}=77^o46'\).