Cho tứ giác ABCD. Phát biểu một điều kiện cần và đủ để :
a) ABCD là một hình bình hành
b) ABCD là một hình chữ nhật
c) ABCD là một hình thoi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mệnh đề P ⇒ Q là "Nếu ABCD là một hình vuông thì nó là một hình bình hành". Mệnh đề này đúng.
b) Mệnh đề P ⇒ Q là "Nếu ABCD là một hình thoi thì ABCD là một hình chữ nhật". Mệnh đề này sai.

E, F lần lượt là trung điểm của AB và BC (gt)
\(\Rightarrow\) EF là đường trung bình của tam giác ABC
\(\Rightarrow\) EF // AC và EF = \(\frac{1}{2}\) AC (1)
H, G lần lượt là trung điểm của AD và DC (gt)
\(\Rightarrow\) HG là đường trung bình của tam giác ACD
\(\Rightarrow\) HG // AC và HG = \(\frac{1}{2}\) AC (2)
Từ (1) và (2) \(\Rightarrow\) EF // HG và EF = HG
\(\Rightarrow\) Tứ giác EFGH là hình bình hành
Tứ giác EFGH là hình bình hành. EF // AC, EF = \(\frac{1}{2}\) AC
Ta còn có EH là đường trung bình của tam giác ABD
\(\Rightarrow\) EH // BD và EH = \(\frac{1}{2}\) BD
- Tứ giác EFGH là hình chữ nhật
\(\Leftrightarrow\) Hình bình hành EFGH có:
\(\widehat{HEF}=90^o\)
\(\Leftrightarrow HE\perp EF\)
\(\Leftrightarrow EH\perp AC\)
\(\Leftrightarrow AC\perp BD\)
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc với nhau thì tứ giác EFGH là hình chữ nhật
- Tứ giác EFGH là hình thoi
\(\Leftrightarrow\) Hình bình hành EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD bằng nhau thì tứ giác EFGH là hình thoi
- Tứ giác EFGH là hình vuông
\(\Leftrightarrow\) Hình chữ nhật EFGH có: EF = EH \(\Leftrightarrow\) AC = BD
Vậy tứ giác ABCD cần thêm điều kiện hai đường chéo AC và BD vuông góc và bằng nhau thì tứ giác EFGH là hình vuông

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành

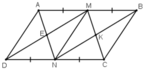
ABCD là hình bình hành ⇒ AB = CD.
M là trung điểm AB ⇒ AM = MB = AB/2.
N là trung điểm CD ⇒ CN = DN = CD/2.
⇒ AM = MB = CN = DN.
+ Tứ giác BMDN có: BM // DN và BM = DN
⇒ BMDN là hình bình hành
⇒ DM // BN hay ME // NK
+ Tứ giác AMCN có: AM // NC, AM = NC
⇒ AMCN là hình bình hành
⇒ AN // CM hay EN // MK.
+ Tứ giác MENK có: ME // NK và NE // MK
⇒ MENK là hình bình hành.
a) MENK là hình thoi
⇔ MN ⊥ EK.
⇔ CD ⊥ AD (Vì EK // CD và MN // AD)
⇔ ABCD là hình chữ nhật.
b) MENK là hình chữ nhật
⇔ MN = EK
Mà MN = BC; 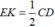 (vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
(vì tam giác MCD có E và K lần lượt là trung điểm MD, MC nên EK là đường trung bình của tam giác MCD).
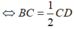
⇔ CD = 2.BC.
c) MENK là hình vuông
⇔ MENK là hình thoi và đồng thời là hình chữ nhật
⇔ ABCD là hình chữ nhật và có CD = 2.BC.
a) Tứ giác ABCD là một hình bình hành khi và chỉ khi AB // CD và AB = CD
b) Tứ giác ABCD là một hình chữ nhật khi và chỉ khi nó là một hình bình hành và có một góc vuông
c) Tứ giác ABCD là một hình thoi khi và chỉ khi nó là một hình bình hành và có hai đường chéo vuông góc với nhau