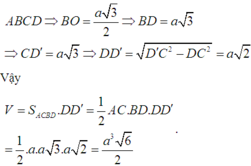cho hình lăng trụ ABC và A'B'C gọi h là trung điểm của A'B'
a) tìm giao tuyến của (AB'C') với(BA'C')
b) chứng minh CB'// (AHC')
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 2 2017
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
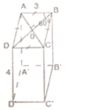
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
CM
20 tháng 10 2018
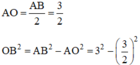
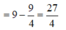
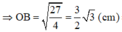
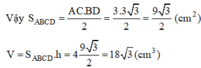
Đáp án B.
Hình trụ ngoại tiếp hình lăng trụ ABC.A’B’C’ có chiều cao AA’; tâm của đáy là trung điểm của AC nên
CM
13 tháng 9 2018
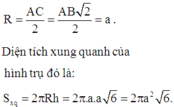
Đường cao của hình lăng trụ là CC' = 25 a 2 - 16 a 2 = 3a
Do đó V = 3a. 1 2 . 3 a . 4 a = 18 a 3
Đáp án A
CM
24 tháng 7 2018
Đáp án A
∆ A B C cân tại B(BA = BC = a) có A B C ^ = 60 0 nên đều. Gọi O là tâm của hình thoi
