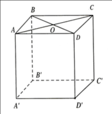
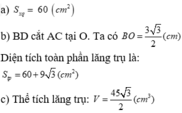Cho hình lăng trụ và hình chóp có diện tích đáy và chiều cao bằng nhau. Tính tỉ số thể tích của chúng ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VD
Võ Đông Anh Tuấn
1 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
CM
11 tháng 5 2018
Gọi S là diện tích đáy và h là chiều cao của hình lăng trụ và của hình chóp, ta có:
PN
2 tháng 10 2017
Hướng dẫn giài:
Gọi B là diện tích đáy và h là chiều cao ta có:
\(V_{chop}=\frac{1}{3}Bh\)
\(V_{tl}=Bh\)
\(\Rightarrow\frac{V_{chop}}{V_{tl}}=\frac{\frac{1}{3}Bh}{Bh}=\frac{1}{3}\)
AH
Akai Haruma
Giáo viên
21 tháng 5 2022
Lời giải:
Diện tích đáy: $5.5=25$ (cm2)
Thể tích hình lăng trụ: $25\times 7=175$ (cm3)
Diện tích xung quanh hình lăng trụ:
$4.5.7=140$ (cm2)
TT
10 tháng 5 2021
vì 2 đường chéo của hình thoi vuông góc với nhau và cắt nhau tại trung điểm mỗi đường nên 1 nửa cả 2 đường chéo lần lượt là 3 và 4
vì vuông góc dùng định lý pitago tích cạnh của hình thoi \(\sqrt{3^{2}+4^{2}}=5\)cm
Stp=Sđáy+Sxq
248= 1/2.6.8+5.4.h
=> h=11,2
thể tích hình lăng trụ 6.8.11,2:2=268.8 (tại bạn ko cho đv ban đầu nên mk ko để đv nhé)
CM
23 tháng 2 2017
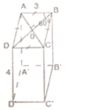
a) Sxq = 2.P.H (p: chu vi đáy; h: chiều cao)
= 3(3 + 3).4 = 48(cm2)
b) Gọi O là giao điểm của AC và BD. Vì tứ giác ABCD là hình thoi nên AC ⊥ BD tại O và có ∠ABC = 60o => ∠ABO = 30o
ΔABO là nửa tam giác đều nên
DD
Đoàn Đức Hà
Giáo viên
26 tháng 3 2022
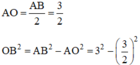
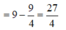
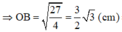
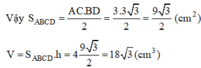
\(S_{ABCD}=\frac{3V_{S.ABCD}}{SO}=\frac{3.16}{3}=16\left(cm^2\right)\)
\(AB=\sqrt{16}=4\left(cm\right)\)
\(H\)là trung điểm \(AB\)
suy ra \(SH\perp AB\).
\(SH=\sqrt{SO^2+OH^2}=\sqrt{3^2+2^2}=\sqrt{13}\)
\(S_{xq}=4.\frac{1}{2}SH.AB=2.\sqrt{13}.4=8\sqrt{13}\left(cm^2\right)\)