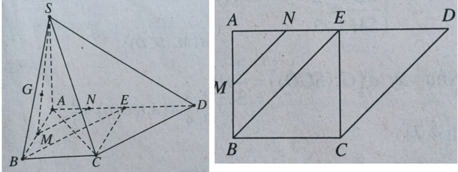
bài 1.cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, đáy lớn AD=2a, đáy nhỏ là BC=a, AB=a, SA vuông góc (ABCD).CMR: a. BC vuông (SAB) b. Tam giác SCD vuông Bài 2: cho hình chóp S.ABCD...

N

Ngân

27 tháng 3 2017

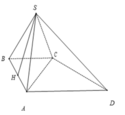
bài 1.cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B, đáy lớn AD=2a, đáy nhỏ là BC=a, AB=a, SA vuông góc (ABCD).CMR: a. BC vuông (SAB) b. Tam giác SCD vuông Bài 2: cho hình chóp S.ABCD có đáy là hình vuông canh a, SA vuông (ABCD). gọi M,N là 2 điểm lần lượt nằm trên cạnh BC và DC sao cho BM=\(\dfrac{a}{2}\) , DN=\(\dfrac{3a}{4}\). CMR: MN vuông (SAM) bài 3:cho tứ diện ABCD có DA vuông (ABC), tam giác ABC cân tại A và AB=AC=a, BC=\(\dfrac{6a}{5}\) ....

Đọc tiếp

#Toán lớp 11

0

VT

Vũ Thị Hà Vy

27 tháng 3 2023

Cho hình chóp S.ABCD có SA vuông góc với đáy. Đáy ABCD là hình thang vuông ở A, B sao cho AB = BC = AD/2 = a. SA = 2a. a. Xác định góc giữa (SAB) và (SCD). b, Xác định góc giữa (SBD) và (SAB). c. Xác định góc giữa (SBC) và (SCD).

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

31 tháng 3 2023

a: Qua S kẻ đường Sx song song SD

=>Sx vuông góc SA

SC vuông góc CD

=>SC vuông góc Sx

((SAB);(SCD))=góc ASC

b: (SBD) căt (SAB)=SB

Kẻ DA vuông góc AB

mà DA vuông góc SA

nên DA vuông góc (SAB)

=>DA vuông góc SB

Kẻ AK vuông góc SB

=>((SBD);(SAB))=góc AKD

c: (SBC) giao (SCD)=SC
Kẻ BH vuông góc SC

Qua H kẻ HF//CD

=>HF vuông góc SC

=>((SBC);(SCD))=góc BHF

Đúng(0)

PT

Pham Trong Bach

24 tháng 6 2019

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B với AB = BC = a, AD = 2a. Cạnh bên SA vuông góc với đáy và SC tạo với (SAD) góc 30 o . Gọi G là trọng tâm tam giác SAB. Tính khoảng cách từ G đến mặt phẳng (SCD).

#Toán lớp 11

1

CM

Cao Minh Tâm

24 tháng 6 2019

Giải sách bài tập Toán 11 | Giải sbt Toán 11

+ Xác định góc của SC với (SAD).

Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .

∠(CSE) cũng chính là góc giữa SC và mp(SAD).

Trong ΔCSE, ta có:

S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .

Nhận xét

Gọi M, N lần lượt là trung điểm của AB và AE.

Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra

d(M,(SCD)) = d(N,(SCD)).

Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))

+ Xác định khoảng cách từ A đến (SCD).

Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.

CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).

Hạ AH ⊥ SC, ta có AH ⊥ (SCD).

Đúng(0)

NM

Nguyễn Mai

25 tháng 4 2023

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A,B với AB=BC=a , AD=2a , SA vuông góc (ABCD) và SA = a√2 a) Cminh các mặt bên của hình chóp là các tam giác vuông

#Toán lớp 11

0

PB

Phương Bùi Hà

15 tháng 5 2020 - olm

Bài 4. Cho hình chóp S.ABC , hình chiếu của S lên mặt phẳng (ABC) là trung điểm H của AC, đáy ABC là tam giác vuông ở B, SA = 2a, AB = av3, BC = a. Tính góc (SH,(SAB)). Bài 5. Cho hình chóp S.ABCD, SA1(ABCD), đáy ABCD là hình vuông cạnh a, góc giữa mặt phăng (SBC) và (ABCD) bằng 30°. Tính góc (AD.(SCD)).

#Toán lớp 11

1

TV

trần văn hải

23 tháng 5 2020

3+? =2 trả lời đc thì giải đc

Đúng(0)

NC

Ngô Chí Thành

4 tháng 5 2021

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B . AD=a, AB=2a,BC=3a , (SAB) đều và vuông góc với đáy . Tính khoảng cách từ điểm A đến (SCD) .

#Toán lớp 11

0

JE

Julian Edward

21 tháng 4 2021

Cho hình chóp S.ABCD có SA vuông góc với mp đáy (ABCD) và ABCD là hình thang vuông tại A, đáy lớn AB, AB=2a, AD=CD=a. Gọi H là hình chiếu vuông góc của A lên SC và E là trung điểm của ABa, CMR: (SCD) ⊥(SAD) và AH ⊥(SBC)b, Biết góc giữa 2 mp (SCD) và (ABCD) bằng 300. Tính góc giữa 2 mp (SAD) và...

Đọc tiếp

#Toán lớp 11

1

NV

Nguyễn Việt Lâm

Giáo viên

21 tháng 4 2021

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)

\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)

\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)

\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)

\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)

b.

\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)

\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)

Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)

Qua S kẻ đường thẳng d song song AD

Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)

Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)

\(AE=\dfrac{AB}{2}=a\)

\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)

Đúng(2)

JE

Julian Edward

21 tháng 4 2021

\(tan\widehat{ASE}=\sqrt{3}\) chứ aj?

Đúng(0)

PT

Pham Trong Bach

5 tháng 6 2018

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD). A. h = a 3 B. h = a 6 6 C. h = a 6 3 D. h = a 3 6 ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

5 tháng 6 2018

Đáp án B

Đúng(0)

PT

Pham Trong Bach

13 tháng 6 2018

Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A, B và AD = 2a, AB = BC = SA = a. Cạnh bên SA vuông góc với đáy, với M là trung điểm AD. Tính khoảng cách h từ M đến mặt phẳng (SCD).

A. h = a 3

B. h = a 6 6

C. h = a 6 3

D. h = a 3 6

#Mẫu giáo

1