Cho điểm A nằm trong góc nhọn xOy. Từ A kẻ AB vuông góc với Ox, AC vuông góc với Oy. Gọi M, N lần lượt là trung điểm của OA và BC. Chứng minh rằng MN vuông góc với BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 4 2023
a: ΔOAB cân tại O
mà OI là phân giác
nên OI vuông góc AB và OI là trung trực của AB
b: Xét ΔOAB có
OI,AD là đường cao
OI cắt AD tại C
=>C là trực tâm
=>BC vuông góc Ox tại E
c: Xét ΔODA vuông tại D và ΔOEB vuông tại E có
OA=OB
góc DOA chung
=>ΔODA=ΔOEB
=>OD=OE
Xét ΔOAB có OE/OA=OD/OB
nên ED//AB
9 tháng 1 2023
a: Xét ΔOAE vuông tại A và ΔOBF vuông tại B có
OA=OB
góc O chung
Do đó: ΔOAE=ΔOBF
=>OE=OF
b: Xét ΔABE và ΔBAF có
AB chung
BE=AF
AE=BF
Do đó: ΔABE=ΔBAF
=>góc BAE=góc ABF
c: Xét ΔIAB có góc IAB=góc IBA
nên ΔIAB cân tại I
=>IA=IB
mà OA=OB
nên OI là trung trực của AB
=>OI vuông góc với AB
KV
5 tháng 12 2023
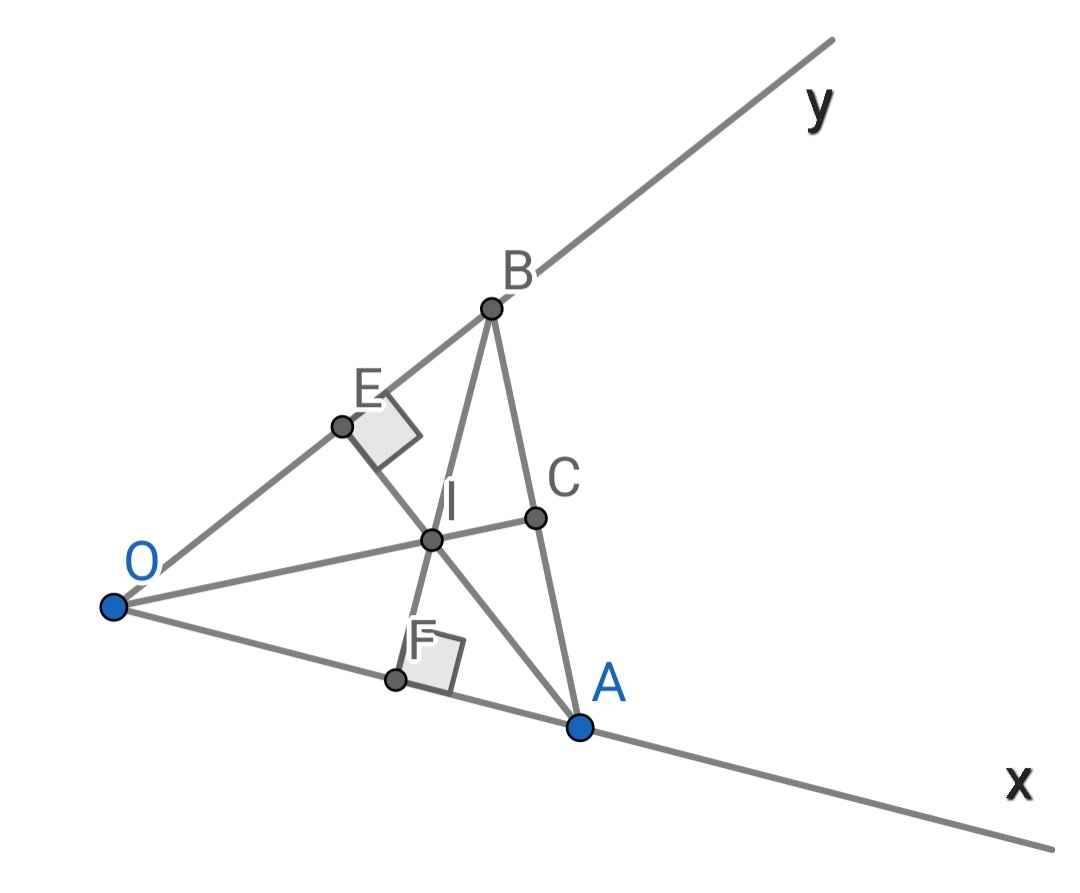a) Xét hai tam giác vuông: ∆OAE và ∆OBF có:
OA = OB (gt)
∠O là góc chung
⇒ ∆OAE = ∆OBF (cạnh huyền - góc nhọn)
⇒ OE = OF (hai cạnh tương ứng)
b) Do OE = OF (cmt)
OB = OA (gt)
⇒ BE = OB - OE
= OA - OF
= AF
Xét hai tam giác vuông: ∆BAE và ∆ABF có:
AB là cạnh chung
BE = AF (cmt)
⇒ ∆BAE = ∆ABF (cạnh huyền - cạnh góc vuông)
⇒ ∠BAE = ∠ABF (hai góc tương ứng)
c) Gọi C là giao điểm của OI và AB
Xét hai tam giác vuông: ∆OIE và ∆OIF có:
OE = OF (cmt)
OI là cạnh chung
⇒ ∆OIE = ∆OIF (cạnh huyền - cạnh góc vuông)
⇒ ∠IOE = ∠IOF (hai góc tương ứng)
⇒ ∠COB = ∠COA
Xét ∆OAC và ∆OBC có:
OC là cạnh chung
∠COA = ∠COB (cmt)
OA = OB (gt)
⇒ ∆OAC = ∆OBC (c-g-c)
⇒ ∠OCA = ∠OCB (hai góc tương ứng)
Mà ∠OCA + ∠OCB = 180⁰ (kề bù)
⇒ ∠OCA = ∠OCB = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AB
⇒ OI ⊥ AB
20 tháng 6 2017
Bài 1 :
Xét tam giác ABC và ADE có :
góc EAD = góc CAB (đối đỉnh)
CA=EA (gt)
BA=DA (gt)
suy ra tam giác ABC=ADE (c.g.c)
suy ra :DE =BC ( 2 cạnh tương ứng ) ; góc E= góc C ; góc D = góc B (các góc tương ứng )
Mà M; N lần lượt là trung điểm của DE và BC suy ra EN=DN=BM=CM
Xét tam giác ENA và CMA có:
EN = CM ( cmt)
góc E = góc C (cmt)
AE = AC (gt)
suy ra tam giác EAN = CMA (c.g.c) suy ra AM =AN ( 2 cạnh tương ứng )
Xét tam giác NDA và MBA có:
góc D= góc B (cmt)
ND = MB (cmt )
DA = BA (cmt )
suy ra tam giác NDA = MBA (c.g.c)suy ra góc NAD = góc MAB
Ta có góc DAC +MAC+MAB = 180 độ ( vì D nằm trên tia đối của tia AB )
Mà góc NAD = góc MAB suy ra góc DAC+MAC+NAD =180 độ
suy ra 3 điểm M,A,N thẳng hàng (2)
Từ (1) và (2 ) suy ra A là trung điểm của MN
( mình vẽ hình hơi xấu , mong bạn thông cảm . Nếu đúng nhớ kết bạn với mình nhé , mong tin bạn ^-^)
17 tháng 6 2022
Bài 3:
Xét ΔHMB vuông tại H và ΔKMC vuông tại K có
MB=MC
\(\widehat{HMB}=\widehat{KMC}\)
Do đo: ΔHMB=ΔKMC
Suy ra: BH=CK