Tổng các nghiệm của phương trình:
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: x 2 - 2 a x - 1 - 1 = 0 ⇔ x 2 - 2 a x + 2 a - 1 = 0
⇔ x = 1 x = 2 a d o 1 + - 2 a + 2 a - 1 = 0
Yêu cầu bài toán x 1 + x 2 = x 1 2 + x 2 2 ⇒ x 1 + x 2 = ( x 1 + x 2 ) 2 − 2 x 1 x 2
⇒ 2 a = 4 a 2 − 4 a + 2 ⇒ a = 1 a = 1 2
Đáp án cần chọn là: A

a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: 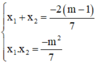
Khi đó:
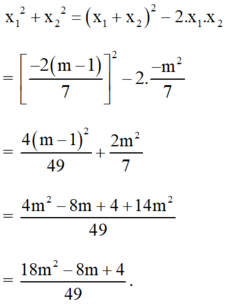


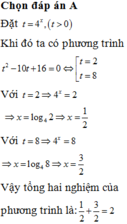
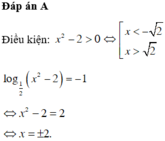
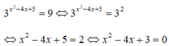
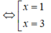


điều kiện xác định:
\(x\ne3;x\ne-3\)\(\dfrac{13-x}{x+3}+\dfrac{6x^2+6}{x^4-8x^2-9}-\dfrac{3x+6}{x^2+5x+6}-\dfrac{2}{x-3}=0\\ \Leftrightarrow\dfrac{13-x}{x+3}+\dfrac{6\left(x^2+1\right)}{\left(x^2-9\right)\left(x^2+1\right)}-\dfrac{3\left(x+2\right)}{\left(x+2\right)\left(x+3\right)}-\dfrac{2}{x-3}=0\\\Leftrightarrow\dfrac{13-x}{x+3}+\dfrac{6}{\left(x-3\right)\left(x+3\right)}-\dfrac{3}{x+3}-\dfrac{2}{x-3}=0\\ \Leftrightarrow\dfrac{\left(13-x\right)\left(x-3\right)+6-3\left(x-3\right)-2\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=0\\ \Leftrightarrow16x-39-x^2+6-3x^{ }+9-2x-6=0\\ \Leftrightarrow-x^2-11x-30=0\\ \Leftrightarrow^{ }-\left(x^2+11x+30\right)=0\\ \Leftrightarrow-\left(x+5\right)\left(x+6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x+5=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-5\left(tmdkxd\right)\\x=-6\left(tmdkxd\right)\end{matrix}\right.\)
Vậy phương trinh có tập nghiệm là S={-5;-6}
cho mình bổ sung ĐKXĐ:\(x\ne-2\)