 Giải chi tiết giúp mk vs
Giải chi tiết giúp mk vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




5: ĐKXĐ: \(\left\{{}\begin{matrix}x^2+3x-4>=0\\2x^2-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left(x+4\right)\left(x-1\right)>=0\\2x\left(x-1\right)>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=1\\x< =-4\end{matrix}\right.\\\left[{}\begin{matrix}x>=1\\x< =0\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x>=1\\x< =-4\end{matrix}\right.\)
\(\sqrt{x^2+3x-4}< \sqrt{2x^2-2x}\)
=>\(x^2+3x-4< 2x^2-2x\)
=>\(2x^2-2x-x^2-3x+4>0\)
=>\(x^2-5x+4>0\)
=>(x-1)(x-4)>0
=>\(\left[{}\begin{matrix}x>4\\x< 1\end{matrix}\right.\)
Kết hợp ĐKXĐ, ta được:
\(\left[{}\begin{matrix}x>4\\x< =-4\end{matrix}\right.\)
7: ĐKXĐ: x>=-1
\(2\sqrt{x+2+2\sqrt{x+1}}-\sqrt{x+1}=4\)
=>\(2\cdot\sqrt{x+1+2\sqrt{x+1}+1}-\sqrt{x+1}=4\)
=>\(2\cdot\sqrt{\left(\sqrt{x+1}+1\right)^2}-\sqrt{x+1}=4\)
=>\(2\left(\sqrt{x+1}+1\right)-\sqrt{x+1}=4\)
=>\(\sqrt{x+1}+2=4\)
=>\(\sqrt{x+1}=2\)
=>x+1=4
=>x=3(nhận)


3: \(\Leftrightarrow\dfrac{x-1}{2x-3}< 0\)
hay 1<x<3/2

câu 2 thì mk có pt nhưng mk ko bt giải
\(\left\{{}\begin{matrix}\dfrac{1}{x}-\dfrac{1}{y}=\dfrac{1}{10}\\x-y=15\end{matrix}\right.\)





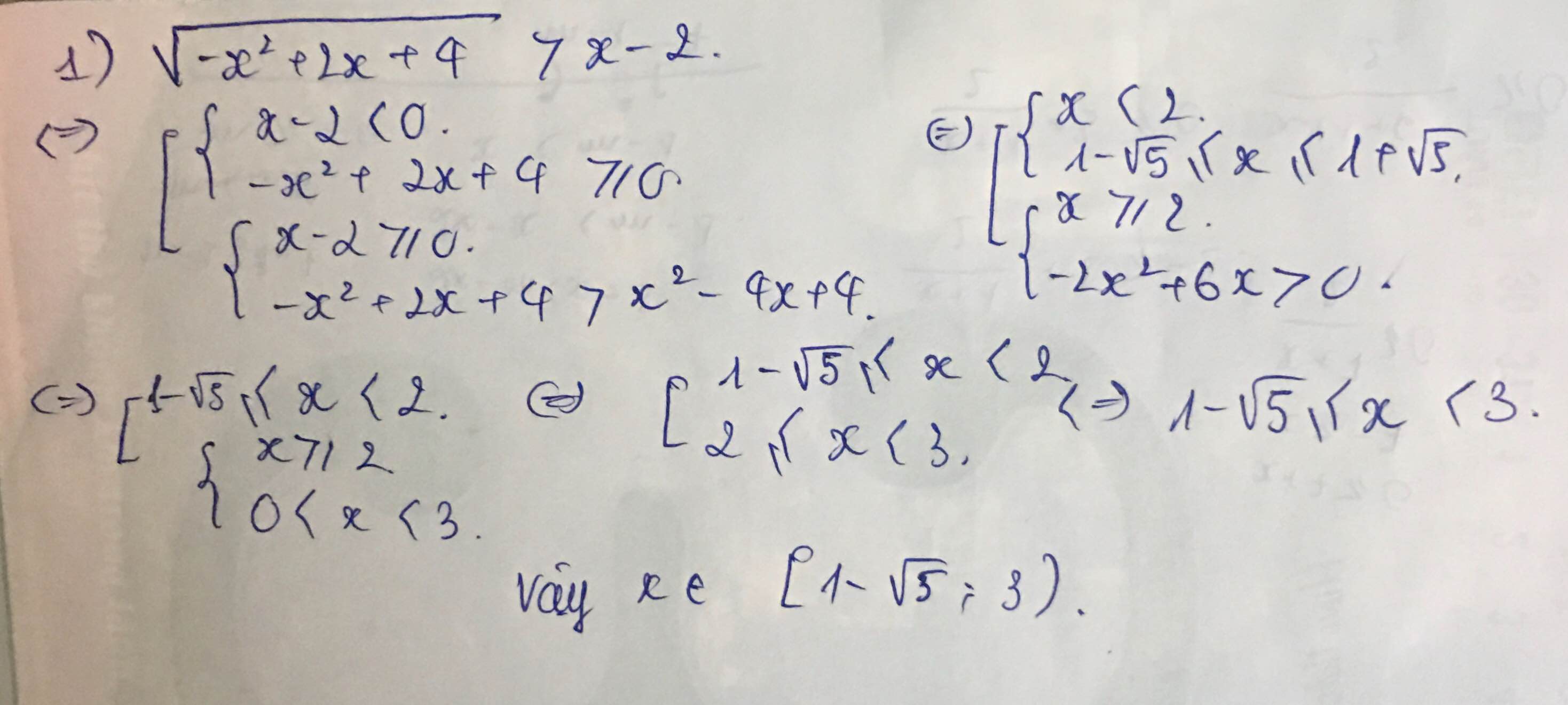

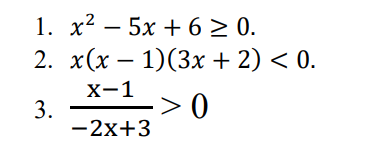

Áp dụng HĐT bình phương của 1 tổng ta có:\(x^2+2xy+y^2=x^2+y^2+2xy=1+2xy\)Ta có: \(\left(x-y\right)^2\ge0\Leftrightarrow x^2-2xy+y^2\ge0\) (HĐT bình phương của 1 hiệu)
\(\Rightarrow2xy\le x^2+y^2\) hay \(2xy\le1\)
\(\Rightarrow\left(x+y\right)^2=1+2xy\le1+1=2\)
\(\Rightarrow MAX_{\left(x+y\right)^2}=2\)
Áp dụng BĐT BCS, ta có:
\(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\)
\(2\ge\left(x+y\right)^2\)
\(\left(x+y\right)^2\le2\)
Vậy: \(Max_{\left(x+y\right)^2}=2\) khi \(x^2+y^2=1\)