a) C/m: Cos15o=\(\dfrac{\sqrt{6}+\sqrt{2}}{4}\)(3 cách)
b) Trục căn thức ở mẫu:
P=\(\dfrac{1}{2+\sqrt[3]{2}+\sqrt[3]{32.cos15^o-10-8\sqrt{3}}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
Nguyễn Đức Trí
VIP
12 tháng 8 2023
Bài 1 :
a) \(Cos30^o=Cos\left(2.15^o\right)=2cos^215^o-1\)
\(\Rightarrow cos^215^o=\dfrac{cos30^o+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\dfrac{\sqrt[]{3}}{2}+1}{2}\)
\(\Rightarrow cos^215^o=\dfrac{\sqrt[]{3}+2}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\sqrt[]{3}+2}}{2}\)
\(\Rightarrow cos15^o=\dfrac{2\sqrt[]{\sqrt[]{3}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{4\sqrt[]{3}+8}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6+2.2\sqrt[]{2}\sqrt[]{6}+2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{\left(\sqrt[]{6}+\sqrt[]{2}\right)^2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt[]{6}+\sqrt[]{2}^{ }}{4}\left(dpcm\right)\)
12 tháng 8 2023
a)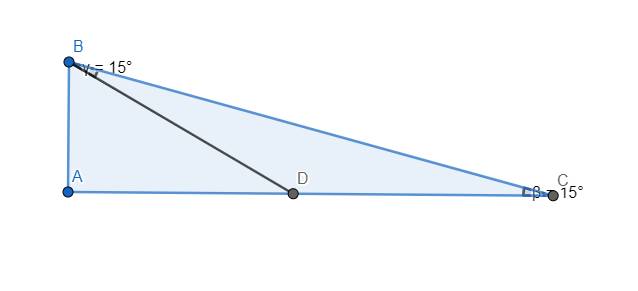
Dựng tam giác ABC vuông tại A với \(\widehat{C}=15^o\). Trên đoạn thẳng AC lấy điểm D sao cho \(\widehat{CBD}=15^o\). Không mất tính tổng quát, ta chuẩn hóa \(AB=1\). \(\Rightarrow\left\{{}\begin{matrix}BD=\dfrac{AB}{cos60^o}=2\\AD=AB.tan60^o=\sqrt{3}\end{matrix}\right.\)
Dễ thấy tam giác DBC cân tại D \(\Rightarrow BD=CD=2\) \(\Rightarrow AC=AD+DC=2+\sqrt{3}\)
\(\Rightarrow tanC=\dfrac{AB}{AC}=\dfrac{1}{2+\sqrt{3}}=2-\sqrt{3}\)
\(\Rightarrow\dfrac{sinC}{cosC}=2-\sqrt{3}\)
\(\Rightarrow sinC=\left(2-\sqrt{3}\right)cosC\)
Mà \(sin^2C+cos^2C=1\)
\(\Rightarrow\left(7-4\sqrt{3}\right)cos^2C+cos^2C=1\)
\(\Leftrightarrow\left(8-4\sqrt{3}\right)cos^2C=1\)
\(\Leftrightarrow cos^2C=\dfrac{1}{8-4\sqrt{3}}=\dfrac{2+\sqrt{3}}{4}\)
\(\Leftrightarrow cosC=\sqrt{\dfrac{2+\sqrt{3}}{4}}\) \(=\dfrac{\sqrt{2+\sqrt{3}}}{2}=\dfrac{\sqrt{8+4\sqrt{3}}}{4}\) \(=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
\(\Rightarrow cos15^o=\dfrac{\sqrt{6}+\sqrt{2}}{4}\)
H9
HT.Phong (9A5)
CTVHS
21 tháng 7 2023
a) \(\sqrt{\dfrac{3-\sqrt{5}}{3+\sqrt{5}}}\)
\(=\sqrt{\dfrac{\left(3-\sqrt{5}\right)^2}{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}}\)
\(=\dfrac{\sqrt{\left(3-\sqrt{5}\right)^2}}{\sqrt{3^2-\left(\sqrt{5}\right)^2}}\)
\(=\dfrac{\left|3-\sqrt{5}\right|}{\sqrt{9-5}}\)
\(=\dfrac{3-\sqrt{5}}{2}\)
b) \(\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}\)
\(=\sqrt{\dfrac{\left(2-\sqrt{3}\right)^2}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}}\)
\(=\dfrac{\sqrt{\left(2-\sqrt{3}\right)^2}}{\sqrt{2^2-\left(\sqrt{3}\right)^2}}\)
\(=\dfrac{\left|2-\sqrt{3}\right|}{\sqrt{4-3}}\)
\(=\dfrac{2-\sqrt{3}}{1}\)
\(=2-\sqrt{3}\)
21 tháng 7 2023
a: \(=\sqrt{\dfrac{\left(3-\sqrt{5}\right)\left(3-\sqrt{5}\right)}{4}}=\dfrac{3-\sqrt{5}}{2}\)
b: \(=\sqrt{\dfrac{\left(2-\sqrt{3}\right)^2}{1}}=2-\sqrt{3}\)
d: \(=\left(-3+3\sqrt{6}+4+2\sqrt{6}-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
=(căn 6-11)(căn 6+11)
=6-121=-115
T
7 tháng 9 2023
\(a,\dfrac{7}{\sqrt{12}}=\dfrac{7\sqrt{3}}{\sqrt{12}\cdot\sqrt{3}}\)
\(=\dfrac{7\sqrt{3}}{\sqrt{36}}=\dfrac{7\sqrt{3}}{6}\)
\(b,\dfrac{3}{2\sqrt{3}}=\dfrac{3\sqrt{3}}{2\sqrt{3}\cdot\sqrt{3}}\)
\(=\dfrac{3\sqrt{3}}{2\cdot3}=\dfrac{3\sqrt{3}}{6}=\dfrac{\sqrt{3}}{2}\)
\(c,\dfrac{1}{5\sqrt{12}}=\dfrac{\sqrt{3}}{5\cdot2\sqrt{3}\cdot\sqrt{3}}\)
\(=\dfrac{\sqrt{3}}{10\cdot3}=\dfrac{\sqrt{3}}{30}\)
\(d,\dfrac{2\sqrt{3}+3}{4\sqrt{3}}=\dfrac{\sqrt{3}\left(2+\sqrt{3}\right)}{4\sqrt{3}}\)
\(=\dfrac{2+\sqrt{3}}{4}\)
ND
Nguyễn Đức Trí
VIP
7 tháng 9 2023
a) \(\dfrac{7}{\sqrt[]{12}}=\dfrac{7}{2\sqrt[]{3}}=\dfrac{7\sqrt[]{3}}{2\sqrt[]{3}.\sqrt[]{3}}=\dfrac{7\sqrt[]{3}}{6}\)
b) \(\dfrac{3}{2\sqrt[]{3}}=\dfrac{\sqrt[]{3}.\sqrt[]{3}}{2\sqrt[]{3}}=\dfrac{\sqrt[]{3}}{2}\)
c) \(\dfrac{1}{5\sqrt[]{12}}=\dfrac{1}{10\sqrt[]{3}}=\dfrac{\sqrt[]{3}}{10\sqrt[]{3}.\sqrt[]{3}}=\dfrac{\sqrt[]{3}}{30}\)
d) \(\dfrac{2\sqrt[]{3}+3}{4\sqrt[]{3}}=\dfrac{\sqrt[]{3}\left(2\sqrt[]{3}+3\right)}{4\sqrt[]{3}.\sqrt[]{3}}=\dfrac{3\left(2+\sqrt[]{3}\right)}{12}=\dfrac{2+\sqrt[]{3}}{4}\)
22 tháng 5 2023
Trước hết, ta cần tính giá trị của a và b trong G và H:
$$G^2 = \frac{1}{a+b} \Rightarrow a+b = \frac{1}{G^2}$$
$$H^2 = 4a - 4\sqrt{ab} + 4b = 4(\sqrt{a} - \sqrt{b})^2 \Rightarrow \sqrt{a} - \sqrt{b} = \frac{H}{2}$$
Từ đó, suy ra được:
$$\sqrt{a} + \sqrt{b} = \frac{1}{G}\sqrt{\frac{1}{G^2} + 4}$$
$$\Rightarrow 2\sqrt{a} = \frac{1}{G}\sqrt{\frac{1}{G^2} + 4} + H$$
$$\Rightarrow a = \left(\frac{1}{G}\sqrt{\frac{1}{G^2} + 4} + H\right)^2/4$$
$$\Rightarrow b = \left(\frac{1}{G}\sqrt{\frac{1}{G^2} + 4} - H\right)^2/4$$
Tiếp theo, ta tính giá trị của F:
$$F = 6\sqrt{3} + \sqrt{2} = 6\sqrt{3} + \sqrt{2}\frac{\sqrt{6}+\sqrt{2}}{2} = 6\sqrt{3} + 3\sqrt{2} + 3\sqrt{6}$$
Cuối cùng, ta tính giá trị của K:
$$K = 2xy\left(2\sqrt{x} + 3\sqrt{y}\right) = 2\sqrt{xy}(4\sqrt{x} + 6\sqrt{y})$$
Vậy, ta đã tính được giá trị của F, G, H và K.
6 tháng 7 2021
a) Ta có: \(\dfrac{1}{\sqrt{5}-\sqrt{3}-\sqrt{2}}\)
\(=\dfrac{\sqrt{5}+\sqrt{3}+\sqrt{2}}{5-\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\dfrac{\sqrt{5}+\sqrt{3}+\sqrt{2}}{5-5-2\sqrt{6}}\)
\(=\dfrac{-\sqrt{5}-\sqrt{3}-\sqrt{2}}{2\sqrt{6}}\)
\(=\dfrac{-\sqrt{6}\left(\sqrt{5}+\sqrt{3}+\sqrt{2}\right)}{12}\)
b) Ta có: \(\dfrac{2}{-1-\sqrt{2}+\sqrt{3}}\)
\(=\dfrac{2\left(-1-\sqrt{2}-\sqrt{3}\right)}{\left(-1-\sqrt{2}\right)^2-3}\)
\(=\dfrac{\left(-1-\sqrt{2}-\sqrt{3}\right)}{\sqrt{2}}\)
\(=\dfrac{-\sqrt{2}-2-\sqrt{6}}{2}\)
24 tháng 10 2021
\(\dfrac{-2}{\sqrt{3}-1}=\dfrac{-2\left(\sqrt{3}+1\right)}{2}=-\sqrt{3}-1\\ \dfrac{\sqrt{5}}{\sqrt{7}-3}=\dfrac{-\sqrt{5}\left(\sqrt{7}+3\right)}{2}\\ \dfrac{3\sqrt{3}-2}{1-2\sqrt{3}}=\dfrac{\left(3\sqrt{3}-2\right)\left(1+2\sqrt{3}\right)}{-11}=\dfrac{\sqrt{3}-16}{11}\\ \dfrac{14}{\sqrt{10}+\sqrt{3}}=\dfrac{14\left(\sqrt{10}-\sqrt{3}\right)}{7}=2\sqrt{10}-2\sqrt{3}\)
AH
Akai Haruma
Giáo viên
4 tháng 7 2021
Lời giải:
a.
\(\frac{1}{\sqrt{5}-\sqrt{3}}=\frac{\sqrt{5}+\sqrt{3}}{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}=\frac{\sqrt{5}+\sqrt{3}}{5-3}=\frac{\sqrt{5}+\sqrt{3}}{2}\)
b.
\(=\frac{2[(\sqrt{3}-(\sqrt{2}-1)]}{[(\sqrt{3}+(\sqrt{2}-1)][\sqrt{3}-(\sqrt{2}-1)]}=\frac{2(\sqrt{3}-\sqrt{2}+1)}{3-(\sqrt{2}-1)^2}=\frac{2(\sqrt{3}-\sqrt{2}+1)}{2\sqrt{2}}\)
\(=\frac{\sqrt{3}-\sqrt{2}+1}{\sqrt{2}}=\frac{\sqrt{6}-2+\sqrt{2}}{2}\)
c.
\(=\frac{5(\sqrt[3]{2^2}-3\sqrt[3]{2}+3^2)}{(\sqrt[3]{2})^3+3^3}=\frac{5(\sqrt[3]{4}+3\sqrt[3]{2}+9)}{29}\)