Cho đường tròn (o) S nằm ngoài đường tròn. Kẻ tiếp tuyến SA và SA' cát tuyến SBC tới đường tròn . Phân giác góc BAC cắt BC ở D, Cắt (O) ở E. Gọi H là giao điểm của OS và AA' , gọi G à giao điểm của OE và BS .
Chứng minh SF.SG=SO.SH và SA^2=SF.SG
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 3 2022
a, Ta có SA = SB (tc tiếp tuyến cắt nhau )
OA = OB = R
Vậy OS là đường trung trực đoạn AB
=> SO vuông AB tại H
b, Vì I là trung điểm
=> OI vuông NS
Xét tứ giác IHSE ta có ^EHS = ^EIS = 900
mà 2 góc này kề, cùng nhìn cạnh ES
Vậy tứ giác IHSE nt 1 đường tròn
=> ^ESH = ^HIO ( góc ngoài đỉnh I )
Xét tam giác OIH và tam giác OSE có
^HIO = ^OSE (cmt)
^O_ chung
Vậy tam giác OIH ~ tam giác OSE (g.g)
\(\dfrac{OI}{OS}=\dfrac{OH}{OE}\Rightarrow OI.OE=OH.OS\)
Xét tam giác OAS vuông tại A ( do SA là tiếp tuyến với A là tiếp điểm), đường cao AH ta có
\(OA^2=OH.OS\)(hệ thức lượng)
\(\Rightarrow OA^2=R^2=OI.OE\)
21 tháng 3 2023
1:
ΔOBC cân tại O
mà OI là trung tuyến
nên OI vuông góc BC
góc OIS=góc OAS=90 độ
=>OIAS nội tiếp
2:
Xet ΔSAO vuông tại A có AH là đường cao
nên SH*SO=SA^2
3:
ΔOAD cân tại O
mà OS là đường cao
nên OS là phân giác của góc AOD
Xét ΔAOS và ΔDOS co
OA=OD
góc AOS=góc DOS
OS chung
=>ΔAOS=ΔDOS
=>góc SDO=90 độ
=>SD là tiếp tuyến của (O)
4: Xet ΔSAK và ΔSIA có
góc SAK=góc SIA
gó ASK chung
=>ΔSAK đồng dạng với ΔSIA
=>SA/SI=SK/SA
=>SA^2=SK*SI
16 tháng 5 2023
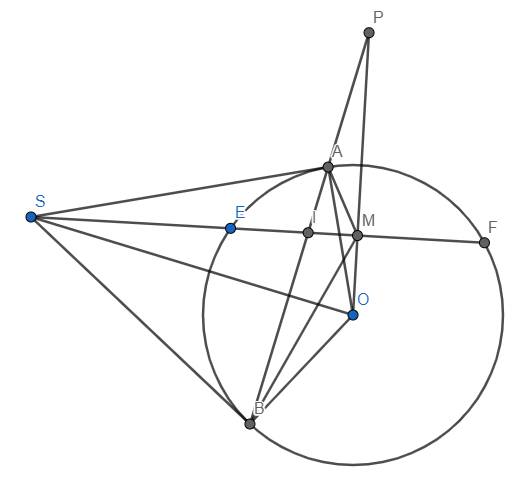
a) Do SA là tiếp tuyến tại A của (O) nên \(\widehat{OAS}=90^o\). Tương tự, ta có \(\widehat{OBS}=90^o\), suy ra \(\widehat{OAS}+\widehat{OBS}=180^o\). Do đó tứ giác SAOB nội tiếp. (đpcm)
Mặt khác, trong đường tròn (O) có M là trung điểm của dây EF nên \(OM\perp EF\) tại M hay \(\widehat{OMS}=90^o\). Từ đó suy ra \(\widehat{OMS}=\widehat{OAS}\),từ đó tứ giác OMAS nội tiếp. Vì vậy 5 điểm O, M, A, S, B cùng thuộc một đường tròn \(\Rightarrow\) Tứ giác SAMO nội tiếp (đpcm)
b) Ta thấy tứ giác OMAB nội tiếp nên \(\widehat{PMA}=\widehat{PBO}\). Từ đó dễ dàng suy ra \(\Delta PAM~\Delta POB\left(g.g\right)\Rightarrow\dfrac{PA}{PO}=\dfrac{PM}{PB}\) \(\Rightarrow PA.PB=PO.PM\) (đpcm)
c) Do tứ giác SAMB nội tiếp nên \(\widehat{SMB}=\widehat{SAB}\) và \(\widehat{SMA}=\widehat{SBA}\). Mặt khác, trong đường tròn (O), có 2 tiếp tuyến tại A và B cắt nhau tại S nên \(SA=SB\) hay \(\Delta SAB\) cân tại S \(\Rightarrow\widehat{SAB}=\widehat{SBA}\) \(\Rightarrow\widehat{SMB}=\widehat{SMA}\) hay MI là phân giác trong của \(\widehat{AMB}\) . Lại có \(MP\perp MI\) nên MP là phân giác ngoài của \(\widehat{AMB}\). Áp dụng tính chất đường phân giác, ta thu được \(\dfrac{IA}{IB}=\dfrac{MA}{MB}\) và \(\dfrac{PA}{PB}=\dfrac{MA}{MB}\). Từ đây suy ra \(\dfrac{IA}{IB}=\dfrac{PA}{PB}\) \(\Rightarrow PA.IB=PB.IA\) (đpcm)
12 tháng 5 2022
Xét tứ giác SAOB có \(\widehat{OAS}+\widehat{OBS}=180^0\)
nên SAOB là tứ giác nội tiếp
Cho đường tròn tâm (O). Từ điểm S ở ngoài đường tròn (O) kẻ các tiếp tuyến SA và SB với (O) (A, B là các tiếp điểm). Kẻ cát tuyến SCD không đi qua tâm O (C nằm giữa S và D). Gọi I là trung điểm của CD.a/ Chứng minh các điểm S, A, I, O, B cùng nằm trên một đường tròn.b/ Chứng minh IS là đường phân giác của góc AIB.c/ Gọi M là giao điểm của hai đường thẳng SO và AB; N là giao điểm của hai đường thẳng SD và AB. Chứng minh MC.ND = NC.MD