Cho tam giác OAB vuông cân tại O, cạnh OA a = . Tính 2OA-OB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DL
1
AH
Akai Haruma
Giáo viên
26 tháng 12 2023
Lời giải:
\(A=|3\overrightarrow{OA}+4\overrightarrow{OB}|\\ \Rightarrow A^2=9OA^2+16OB^2+24\overrightarrow{OA}.\overrightarrow{OB}\)
\(A^2=9a^2+16.2a^2+\overrightarrow{OA}(\overrightarrow{OA}+\overrightarrow{AB})=41a^2+OA^2+\overrightarrow{OA}.\overrightarrow{AB}\\ =41a^2+a^2+0=42a^2\)
(do $OA, AB$ vuông góc với nhau)
$\Rightarrow A=\sqrt{42}a$
VN
0
CM
30 tháng 8 2019
Đáp án: C.
§ Hướng dẫn giải:
Dễ thấy h = 4a và r = 3a.
Kết luận diện tích xung quanh là:
S x q = πrl = πr r 2 + h 2 = 15 πa 2
22 tháng 1
a: Xét ΔKAB vuông tại K và ΔHBA vuông tại H có
BA chung
\(\widehat{KAB}=\widehat{HBA}\)(ΔOAB cân tại O)
Do đó: ΔKAB=ΔHBA
b: Ta có: ΔKAB=ΔHBA
=>\(\widehat{KBA}=\widehat{HAB}\)
=>\(\widehat{IAB}=\widehat{IBA}\)
=>ΔIAB cân tại I
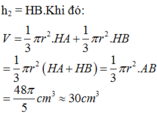
tam giác OAB vuông cân tại O \(\Rightarrow\)OA = OB = a.
2OA - OB = 2OA - OA = OA =a
\(2\cdot OA-OB=2\cdot OA-OA=OA=a\)