1) Tìm x thuộc tập hợp N
a) 16x < 1284
b) 5x . 5x+1 . 5x+2 < 100...0 218
có 18 chữ số 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 7 2023
a: =>2^4x<2^28
=>4x<28
=>x<7
b: =>5^3x+3<5
=>3x+3<1
=>3x<-2
=>x<-2/3
9 tháng 8 2021
Bạn thử xem lại đề nhé, giữa 3 số này là dấu cộng hay dấu nhân.
Nếu là dấu cộng thì ta có:
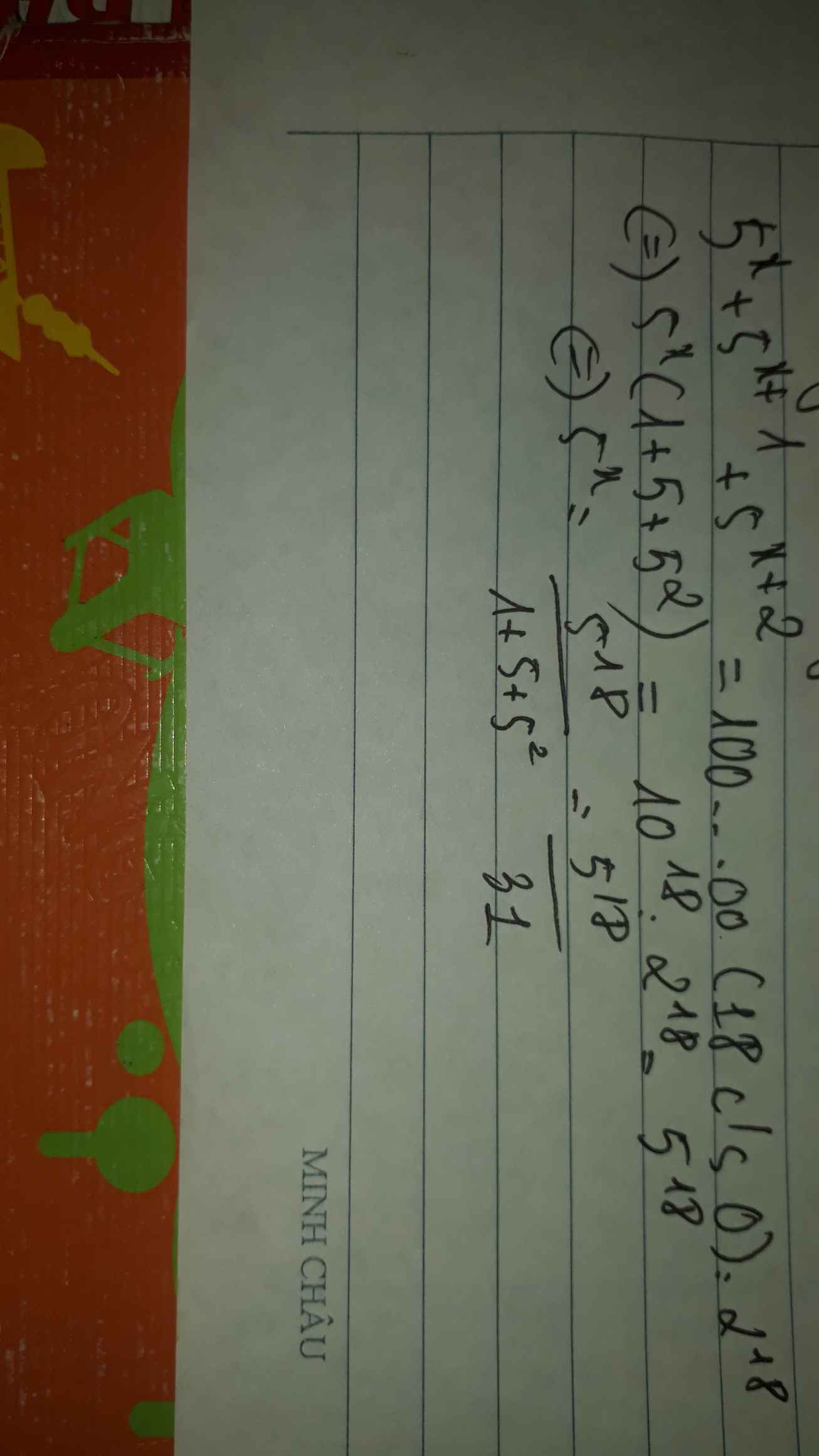
Nếu là dấu nhân thì ta có:
NP
5
T
11 tháng 6 2019
#)Giải :
Câu 1 :
5x(1 - 2x ) - 3x ( x+18) = 0
<=> 5x - 10x^2 - 3x^2 - 54x = 0
<=> -13x^2 - 49x = 0
<=> x= 0 hoặc x = - 49/13
Vậy x có hai giá trị là 0 và - 49/13
JH
0
KH
1
18 tháng 8 2021
a, \(16x^2-9\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(4x\right)^2-\left(3x+3\right)^2=0\Leftrightarrow\left(4x-3x-3\right)\left(4x+2x+3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(6x+3\right)=0\Leftrightarrow x=-\frac{1}{2};x=3\)
b, \(\left(5x-4\right)^2-49x^2=0\Leftrightarrow\left(5x-4-7x\right)\left(5x-4+7x\right)=0\)
\(\Leftrightarrow\left(-2x-4\right)\left(12x-4\right)=0\Leftrightarrow x=-2;x=\frac{1}{3}\)
c, \(5x^3-20x=0\Leftrightarrow5x\left(x^2-4\right)=0\)
\(\Leftrightarrow5x\left(x-2\right)\left(x+2\right)=0\Leftrightarrow x=0;x=\pm2\)
JH
1
18 tháng 8 2021
1: Ta có: \(16x^2-9\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(4x-3x-3\right)\left(4x+3x+3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left(7x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{7}{3}\end{matrix}\right.\)
2: Ta có: \(\left(5x-4\right)^2-49x^2=0\)
\(\Leftrightarrow\left(5x-4-7x\right)\left(5x-4+7x\right)=0\)
\(\Leftrightarrow\left(2x+4\right)\left(12x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3: Ta có: \(5x^3-20x=0\)
\(\Leftrightarrow5x\left(x-2\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)