Cho một hình ngũ giác. Có ba đường thẳng d1, d2, d3 cắt nhau tại ba điểm A, B, C thuộc miền trong ngũ giác sao cho mỗi đường thẳng chia ngũ giác thành hai phần có diện tích bằng nhau. Chứng minh rằng diện tích \(\Delta\)ABC nhỏ hơn \(\dfrac{1}{4}\) diện tích ngũ giác đã cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Tọa độ A là:
\(\left\{{}\begin{matrix}x+2=-x-2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=-4\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=-2+2=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x+2=-2x+2\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=0\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=0+2=2\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}-x-2=-2x+2\\y=-x-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=4\\y=-4-2=-6\end{matrix}\right.\)
Vậy: A(-2;0); B(0;2); C(4;-6)
b: \(AB=\sqrt{\left(0+2\right)^2+\left(2-0\right)^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(4+2\right)^2+\left(-6-0\right)^2}=6\sqrt{2}\)
\(BC=\sqrt{\left(4-0\right)^2+\left(-6-2\right)^2}=\sqrt{4^2+8^2}=4\sqrt{5}\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=0\)
=>\(\widehat{BAC}=90^0\)
=>ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\sqrt{2}\cdot6\sqrt{2}=12\)

a: 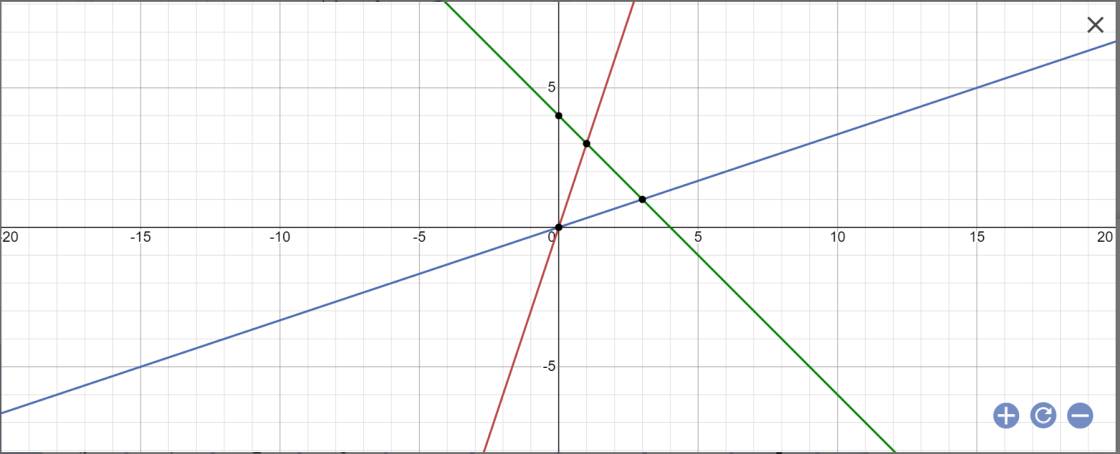
b:
Bổ sung đề: A,B lần lượt là giao của (d1) với (d2) và (d3)
Tọa độ A là:
3x=1/3x và y=3x
=>x=0 và y=0
Tọa độ B là:
3x=-x+4 và y=3x
=>x=1 và y=3

999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999


Giải
Ba đường thẳng d1, d2, d3 cắt nhau tại ba điểm A, B, C chia ngũ giác thành bảy phần với các diện tích được ký hiệu như trên hình
Ta thấy:
S3 + S2 + S7 = \(\dfrac{1}{2}\)S
= S1 + S2 + S7 + S6
S3 = S1 + S6 (1)
Ta cũng có:
\(\dfrac{1}{2}\)S = S1 + S2 + S3 + S4 (2)
Thay (1) vào (2) ta được:
\(\dfrac{1}{2}\)S = 2S1 + S2 + S3 + S4 + S6 > 2S1
Tức là S1 < \(\dfrac{1}{4}\)S