Cho tam giác ABC có đường cao ha; hb; hc tỉ lệ với 4; 5; 6.Biết chu vi của tam giác là 37cm. Tính độ dài cạnh nhỏ nhất của tam giác ABC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 4 2019
Chọn A.
Áp dụng định lí cosin trong tam giác ta có:
a2 = b2 + c2 = 2bc.cosA = 72 + 52 - 2.7.5.3/5 = 32
Nên 
Mặt khác: sin2A + cos2A = 1 nên sin2A = 1 - cos2A = 16/25
Mà sinA > 0 nên sinA = 4/5
Mà: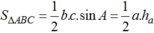 
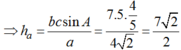
HA
11 tháng 3 2020
A B C H E 1 2 4 3
TA CÓ HAI ĐỌC THẲNG AE VÀ BC CẮT NHAU TẠI H VÀ CÓ MỘT GÓC BẰNG 90
\(\Rightarrow\widehat{H_1}=\widehat{H_2}=\widehat{H_3}=\widehat{H_4}=90\)
XÉT \(\Delta BAH\)VÀ\(\Delta BEH\)CÓ
BH LÀ CẠNH CHUNG
\(\widehat{H_1}=\widehat{H_2}\left(CMT\right)\)
\(AH=EH\left(GT\right)\)
\(\Rightarrow\Delta BAH=\Delta BEH\left(C-G-C\right)\)
\(\Rightarrow AB=BE\)
VẬY \(\Delta BAE\)CÂN TẠI B(ĐPCM)
XÉT \(\Delta ACH\)VÀ\(\Delta ECH\)CÓ
CH LÀ CẠNH CHUNG
\(\widehat{H_1}=\widehat{H_3}\left(CMT\right)\)
\(AH=EH\left(GT\right)\)
\(\Rightarrow\Delta ACH=\Delta ECH\left(C-G-C\right)\)
\(\Rightarrow AC=EC\)
VẬY \(\Delta CAE\)CÂN TẠI C (ĐPCM)
8 tháng 10 2021
a) Xét tam giác ABC có:
\(\left\{{}\begin{matrix}AB^2+AC^2=9^2+12^2=225\\BC^2=15^2=225\end{matrix}\right.\)
\(\Rightarrow AB^2+AC^2=BC^2\)
=> Tam giác ABC vuông tại A(Pytago đảo)
b) Áp dụng tslg trong tam giác ABC vuông tại A:
\(\left\{{}\begin{matrix}sinC=\dfrac{AB}{BC}=\dfrac{9}{15}=\dfrac{3}{5}\\sinB=\dfrac{AC}{BC}=\dfrac{12}{15}=\dfrac{4}{5}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\widehat{C}\approx37^0\\\widehat{B}\approx53^0\end{matrix}\right.\)
c) Áp dụng HTL:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{9.12}{15}=7,2\left(cm\right)\)
\(\left\{{}\begin{matrix}AB^2=BH.BC\\AC^2=CH.BC\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=5,4\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=9,6\left(cm\right)\end{matrix}\right.\)
8 tháng 10 2021
Xét tam giác ABC vuông tại A có Ah đường cao
\(\Rightarrow AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{9.12}{15}=7,2\left(cm\right)\)
\(\Rightarrow AB^2=BH.BC\)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=5,4\left(cm\right)\)
\(\Rightarrow HC=BC-BH=15-5,4=9,6\left(cm\right)\)
HL
25 tháng 10 2016
2S(ABC)=ha.a=hb.b=hc.c suy ra 1/ha+1/hb+1/hc=a/2S+b/2S+c/2S=1/2S .(a+b+c)=1/r(a+b+c) .(a+b+c) =1/r (đpcm) (vì 2S=r(a+b+c))
10 nhe bn!