Câu 9:Cho hai hàm số và
. Tập hợp các giá trị của
để
là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A.
f ' x = − 10 x + 14 − 5 x 2 + 14 x − 9 với 1 < x < 9 5 . f ' x < 0 ⇔ − 10 x + 14 0 ⇔ x 14 10 = 7 5 .
Kết hợp với điều kiện thì x ∈ 7 5 ; 9 5 .

+ Ta có đạo hàm y’ = x2- 2mx+ (m2-1).
Phương trình y’ =0 có ∆ ' = m 2 - ( m 2 - 1 ) = 1 ⇒ x 1 = m - 1 x 2 = m + 1
+ Không mất tính tổng quát, giả sử A ( x 1 ; y 1 ) , B ( x 2 ; y 2 ) .
A, B nằm khác phía khi và chỉ khi x1. x2< 0 hay ( m-1) (m+ 1) < 0
Suy ra -1< m< 1
A, B cách đều đường thẳng y= 5x-9 suy ra trung điểm I của AB nằm trên đường thẳng đó.
Khi đó ta có:
I ( x 1 + x 2 2 ; y 1 + y 2 2 ) h a y I ( m ; 1 3 m 3 - m )
Ta có:
1 3 m 3 - m = 5 m - 9 ⇔ 1 3 m 3 - 6 m + 9 = 0 ⇔ m 1 = 3 1 3 m 2 + m - 3 = 0
Suy ra m 1 + m 2 + m 3 = 3 + - 1 1 3 = 0 .
Chọn A

Đáp án D
y = x 3 − 3 m x 2 + 4 m 3 ⇒ y ' = 3 x 2 − 6 m x . Ta có y ' = 0 ⇔ x = 0 x = 2 m
Để hàm số đã cho có 2 điểm cực trị thì m ≠ 0. Khi đó
y ' = 0 ⇔ x = 0 ⇒ y 0 = 4 m 3 ⇒ A 0 ; 4 m 3 ∈ O y x = 2 m ⇒ y 2 m = 0 ⇒ B 2 m ; 0 ∈ O x
Vậy tam giác OAB vuông tại O nên S Δ O A B = 1 2 O A . O B ⇔ 4 = 1 2 4 m 3 2 m
⇔ m 4 = 1 ⇔ m = − 1 m = 1 ⇒ S − 1 ; 1

Chọn đáp án D
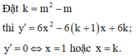
Đồ thị hàm số có hai điểm cực trị khi và chỉ khi k ≠ 1
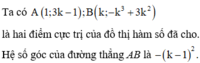
Đường thẳng AB vuông góc với đường thẳng y = x + 2 khi và chỉ khi


1) \(y=\dfrac{2x^2+1}{x^2}\)
\(\Rightarrow y'=\dfrac{\left(4x+1\right)x^2-2x\left(2x^2+1\right)}{x^4}\)
\(\Leftrightarrow y'=\dfrac{4x^3+x^2-4x^3-2x}{x^4}\)
\(\Leftrightarrow y'=\dfrac{x^2-2x}{x^4}=\dfrac{x\left(x-2\right)}{x^4}=\dfrac{x-2}{x^3}\)
2) \(f\left(x\right)=\sqrt[]{-5x^2+14x-9}\)
\(\Rightarrow f'\left(x\right)=\dfrac{-10x+14}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-2\left(5x-7\right)}{2\sqrt[]{-5x^2+14x-9}}\)
\(\Leftrightarrow f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}\)
Để \(f'\left(x\right)=0\)
\(f'\left(x\right)=\dfrac{-\left(5x-7\right)}{\sqrt[]{-5x^2+14x-9}}=0\)
\(\Leftrightarrow5x-7=0\)
\(\Leftrightarrow5x=7\)
\(\Leftrightarrow x=\dfrac{7}{5}\)
Vậy tập hợp giá trị để \(f'\left(x\right)=0\) là \(\left\{\dfrac{7}{5}\right\}\)
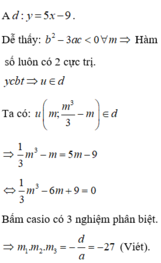
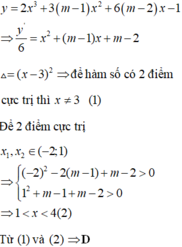
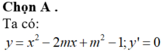



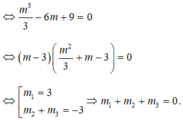

x=[0;4]