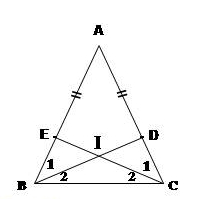
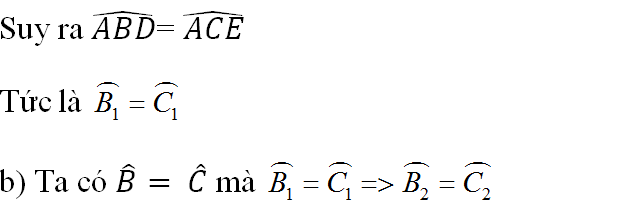Cho tam giác ABC vuông tại A. Trên cạnh AC lấy điểm D sao cho \(\widehat{ABC}=3.\widehat{ABD}\), trên cạnh AB lấy điểm E sao cho \(\widehat{ACB}=3.\widehat{ACE.}\) Gọi F là giao điểm của BD và CE. I là giao điểm của các tia phân giác của \(\widehat{BCF}\) và \(\widehat{CBF}.\)
a, Tính \(\widehat{BFC}\)
b, Chứng minh rằng : Tam giác DEI là tam giác đều