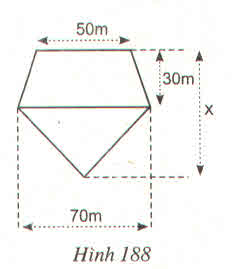
Tính x, biết đa giác ở hình 188 có diện tích là 3375m2
Bài 32 trang 161 SBT toán 8 tập 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải
a) Diện tích hình chữ nhật ABCD gồm:
8 × 4 = 32 (ô vuông)
Diện tích hình tam giác MDC gồm 12 ô vuông và 8 nửa ô vuông (4 ô vuông), tức là gồm:
12 + 4 = 16 (ô vuông)
Diện tích hình chữ nhật ABCD gấp diện tích hình tam giác MDC số lần là:
32 : 16 = 2 (lần)
b) Diện tích hình chữ nhật IKCD gồm:
8 × 2 = 16 (ô vuông)
Diện tích hình chữ nhật IKCD bằng diện tích hình tam giác MDC.
Nhớ tick mình nhé, chúc bạn học tốt!

Gọi dây đi qua M là AB. Kẻ OH vuông góc AB tại H.
Có MB AB≤2R=10
và quan hệ đường vuông góc và đường xiên.
vậy OH có giá trị lớn nhất bằng OM, khi đó độ dài dây AB nhỏ nhất = 8dm (liên hệ dây cung và khoảng cách đến tâm)
....... Từ đó suy ra kết quả.
a) Dây ngắn nhất đi qua M chính là dây vuông góc với bán kính.
Sau đó áp dụng đl Pytago là ra.
b) Dây dài nhất đi qua M chính là đường kính.

\(a,P=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=1\)
\(b,Q=2x^2-6x=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}-\dfrac{9}{4}\right)=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(c,M=\left(x^2-x+\dfrac{1}{4}\right)+\left(y^2+6y+9\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\left(y+3\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\\y=-3\end{matrix}\right.\)
a: Ta có: \(P=x^2-2x+5\)
\(=x^2-2x+1+4\)
\(=\left(x-1\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi x=1

a, Chu vi hình chữ nhật ABCD là :
(45 + 15) *2 = 120 (cm)
Chiều dài cạnh EB là :
45 - 15 = 30 (cm)
b, Diện tích hình thang EBCD là :
(30 + 45) *15 /2 = 562.5 (cm2)
Độ dài cạnh BM hoặc MC là :
15 / 2 = 7.5 (cm)
Diện tích tam giác EBM là :
7.5 * 30 / 2 = 112.5 (cm2)
Tổng diện tích tam giác EBM và DMC là :
7.5 *45 /2 = 168.75 (cm2)
c, Diện tích tam giác EDM là :
562.5 - 281.25 = 281.25 (cm2)
Đáp số : a, 120 cm ; b, 562.5 cm2 ; c, 281.25 cm2