Help mình đang cần gấp

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 4:
\(a,\sqrt{64.\left(x-1\right)^2}=16\\ \Leftrightarrow8\sqrt{\left(x-1\right)^2}=16\\ \\ \Leftrightarrow\sqrt{\left(x-1\right)^2}=\dfrac{16}{8}=2\\ \left|x-1\right|=2\\ \Leftrightarrow\left[{}\begin{matrix}x-1=2\\x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\end{matrix}\right.\\ b,\sqrt{4\left(x-2\right)}=8\\ \Leftrightarrow2\sqrt{x-2}=8\\ \Leftrightarrow\sqrt{x-2}=\dfrac{8}{2}=4\\ \Leftrightarrow x-2=4^2=16\\ \Leftrightarrow x=16+2=18\\ c,\dfrac{\sqrt{2x}}{\sqrt{8}}=5\\ \Leftrightarrow\dfrac{\sqrt{2}\sqrt{x}}{2\sqrt{2}}=5\\ \Leftrightarrow\dfrac{\sqrt{x}}{2}=5\\ \Leftrightarrow\sqrt{x}=5.2=10\\ \Leftrightarrow x=10^2=100\)
Bài 2:
\(a,\left(\sqrt{75}-2\sqrt{12}-\sqrt{27}\right).\sqrt{3}\\ =\left(\sqrt{3.5^2}-2.\sqrt{3.2^2}-\sqrt{3.3^2}\right).\sqrt{3}\\ =\left(5\sqrt{3}-2.2\sqrt{3}-3\sqrt{3}\right).\sqrt{3}\\ =-2\sqrt{3}.\sqrt{3}=-2.3=-6\\ b,\left(5\sqrt{2}-\sqrt{8}-\sqrt{98}\right):\sqrt{2}\\ =\left(5\sqrt{2}-\sqrt{2^2.2}-\sqrt{2.7^2}\right):\sqrt{2}\\ =\left(5\sqrt{2}-2\sqrt{2}-7\sqrt{2}\right):\sqrt{2}\\ =-4\sqrt{2}:\sqrt{2}=-4\)
\(c,\\ \dfrac{\sqrt{18}}{\sqrt{2}}=\sqrt{\dfrac{18}{2}}=\sqrt{9}=\sqrt{3^2}=3\\ d,\\ \sqrt{\dfrac{45}{7}}.\sqrt{\dfrac{28}{5}}=\sqrt{\dfrac{45.28}{7.5}}=\sqrt{\dfrac{9.5.4.7}{7.5}}=\sqrt{9.4}=\sqrt{36}=\sqrt{6^2}=6\)

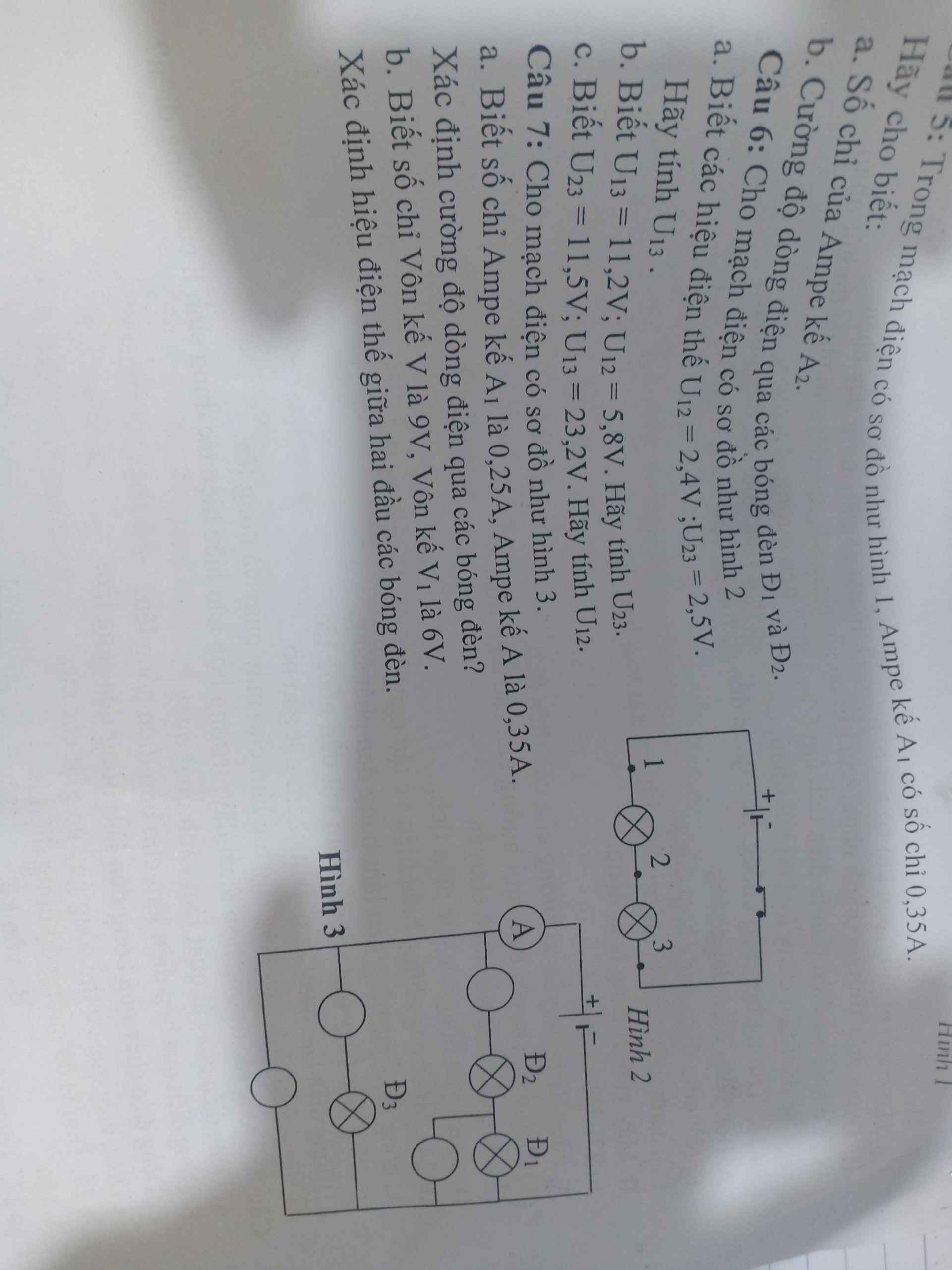
Câu 6)
\(U_{13}=U_{12}+U_{23}=2,4+2,5=4,9V\\ U_{23}=U_{13}-U_{12}=5,4V\\ U_{12}=U_{13}-U_{23}=11,7V\)
Câu 7)
\(I_1=I_2=0,25A\\ I_3=I-I_1\left(I_2\right)=0,1A\\ U=U_1=U_3=9V\\ U_2=U-U_1=3V\)

Số lượng số hạng của dãy số trừ 1 đầu:
\(\left(99-1\right):1+1=99\) (số hạng)
Tổng của dãy số là:
\(\left(99+1\right)\cdot99:2+1=4951\)
Số số hạng của dãy 1 + 2 + 3 + ... + 89:
89 - 1 + 1 = 89 số:
Tổng là:
1 + (89 + 1) . 89 : 2 = 1 + 45 . 89 = 4006

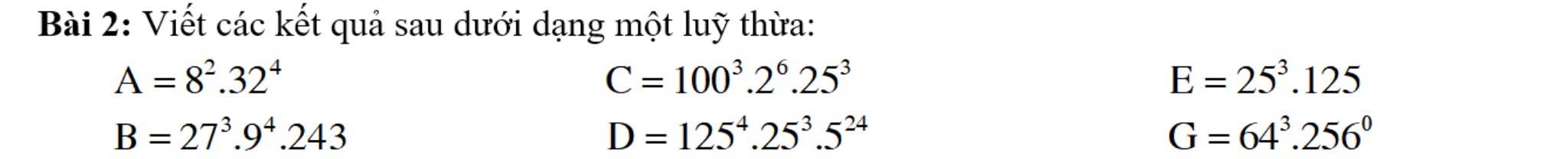 help, mình đang cần gấp
help, mình đang cần gấp mn ơi help mình viowis ạ mình đang cần gấp plssssssss
mn ơi help mình viowis ạ mình đang cần gấp plssssssss

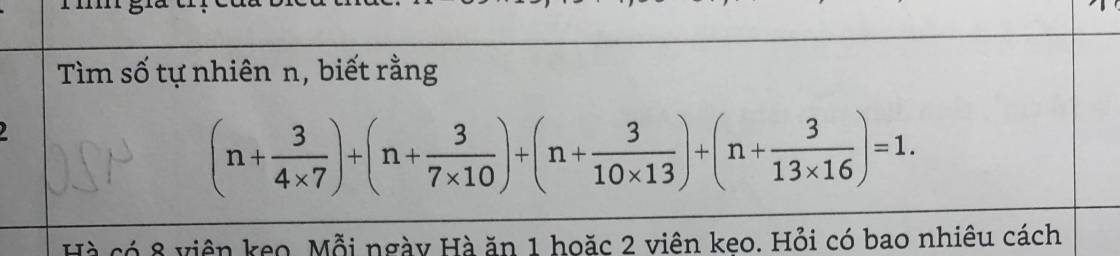

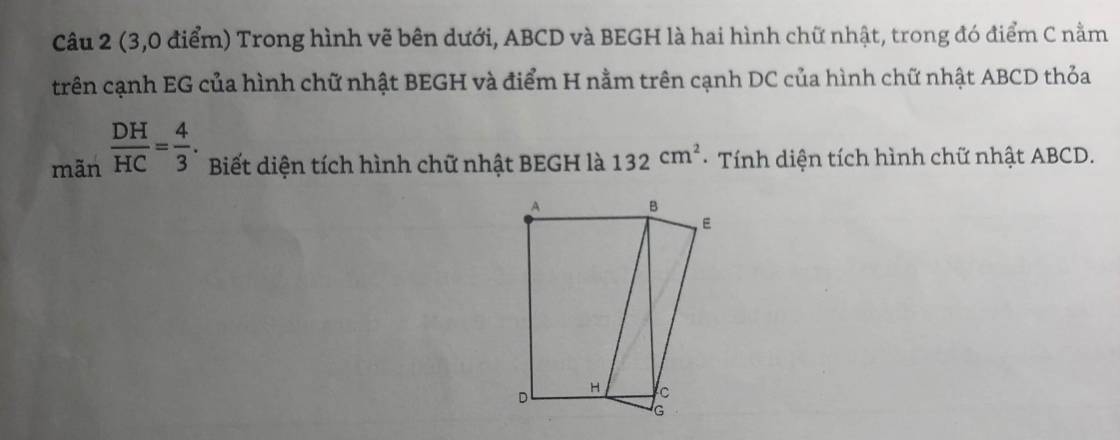
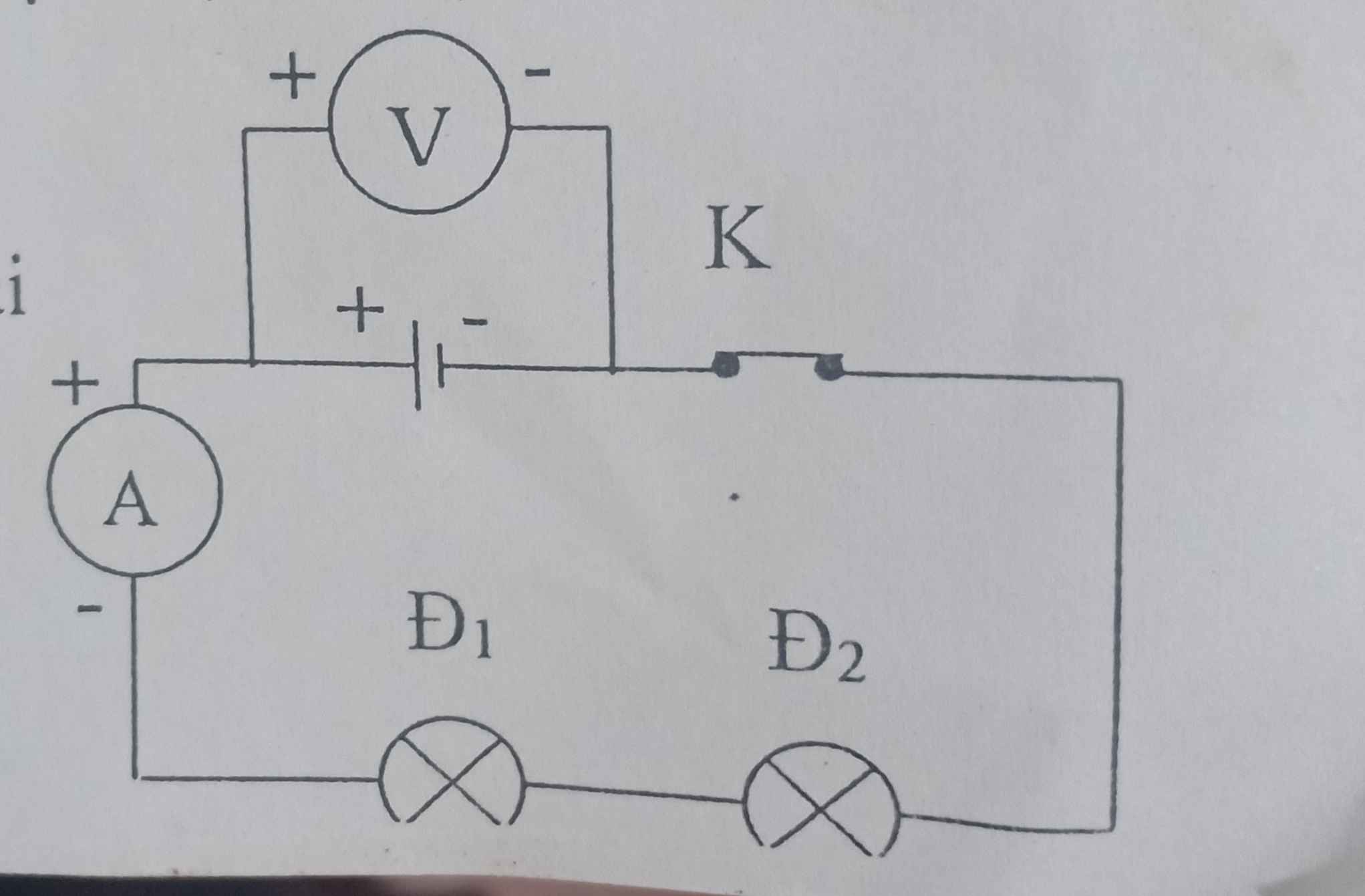
 ai help mk vs mình đang cần gấp mai mk thi gòi plsssssssss
ai help mk vs mình đang cần gấp mai mk thi gòi plsssssssss
Bài 5:
\(A+9=\frac{10}{1}+\frac{10}{2}+\frac{10}{3}+....+\frac{10}{9}\)
\(A=\frac{10}{2}+\frac{10}{2}+\frac{10}{3}+...+\frac{10}{9}+1=\frac{10}{2}+\frac{10}{3}+...+\frac{10}{9}+\frac{10}{10}\)
\(A=10\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{10}\right)=10B\)
$\Rightarrow A:B=10$