 E còn 2c 9,10 nữa ạ
E còn 2c 9,10 nữa ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


9, f'(x) = \(m^3-3m^2+m\) = 3
\(\Rightarrow m\in\left\{1;-1;3\right\}\)

9.
\(f'\left(x\right)=m^3-3m^2+m\) ; \(\forall x\)
\(f'\left(2\right)=m^3-3m^2+m=3\Leftrightarrow m\left(m^2+1\right)-3\left(m^2+1\right)=0\)
\(\Leftrightarrow\left(m-3\right)\left(m^2+1\right)=0\)
\(\Leftrightarrow m=3\)
10.
\(f'\left(x\right)=\dfrac{x+2}{\sqrt{x^2+4x+4}}=\dfrac{x+2}{\left|x+2\right|}=\left[{}\begin{matrix}1\left(x>-2\right)\\-1\left(x< -2\right)\end{matrix}\right.\)
Do \(-4< -2\Rightarrow f'\left(-4\right)=-1\)
Bây giờ chỉ cần kiểm tra 4 giới hạn kia cái nào có kết quả khác -1 là được
Trước hết lưu ý \(\sqrt{x^2+4x+4}=\left|x+2\right|=-x-2\) khi \(x\rightarrow-4\)
Do đó câu A là: \(\lim\limits_{x\rightarrow-4}\dfrac{2x}{-x-2+2}=-2\ne-1\)
Vậy đáp án A

A = (1+2+3+...+98+99)+(0,02+0,03+0,04+...+0,98+0,99+0,100)
= \(\frac{99\left(99+1\right)}{2}\)+ (0,02+0,98)+(0,03+0,97)+(0,04+0,96) +....+(0,49+0,51) +0,50 + 0,100 (có 48 cặp)
= 4950 + 1+1+1+....+1 + 0,6 (có 48 số 1)
= 4950 + 48 + 0,6
= 4998,6
A = 1,2 + 2,3 + 3,4 + ...+ 97,98 + 98,99 + 99,100
= (1 + 2+ 3+ ..+ 97 + 98 + 99) + (0,2 + 0,3 + 0,4 + ...+ 0,98 + 0,99 + 0,100)
Tính 1 + 2+ 3+ ..+ 97 + 98 + 99 = (1+99) x 99 : 2 = 4950
Tính 0,2 + 0,3 + 0,4 + ...+ 0,98 + 0,99 + 0,100
= (0,100 + 0,2 + 0,3 +... + 0,9) + (0,10 + 0,11 + ...+ 0,99)
= (0,1+ 0,9) x 9 : 2 + (0,10 + 0,99) x 90 : 2 = 4,5 + 49,05 = 53,55
Vậy A = 4950 + 53,55 = 5003,55
:D

Bài 10:
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền AB
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=2,4(cm)
Bài 9:
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{A}\) chung
Do đó: ΔABE\(\sim\)ΔACF
Suy ra: \(\dfrac{AB}{AC}=\dfrac{AE}{AF}\)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
\(\widehat{A}\) chung
Do đó: ΔAEF\(\sim\)ΔABC
b: Ta có: \(\dfrac{AE}{AB}=\dfrac{EF}{BC}\)
nên \(BC=EF:\dfrac{1}{2}=5:\dfrac{1}{2}=10\left(cm\right)\)

Bài 9:
\(a,15x^2y^4-M=10x^2y^4+6x^2y^4\\ \Rightarrow M=15x^2y^4-10x^2y^4-6x^2y^4=-x^2y^4\\ Thế.x=-\dfrac{1}{2}.và.y=2.vào.M.thu.gọn:M=-x^2y^4=-\left(-\dfrac{1}{2}\right)^2.2^4=-\dfrac{1}{4}.16=-4\\ b,40x^3y+M=20x^3y+15x^3y\\ \Rightarrow M=20x^3y+15x^3y-40x^3y=-5x^3y\\ Thế.x=-2.và.y=\dfrac{1}{5}.vào.M.thu.gọn:M=-5x^3y=-5.\left(-2\right)^3.\dfrac{1}{5}=-5.8.\dfrac{1}{5}=-8\)


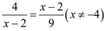

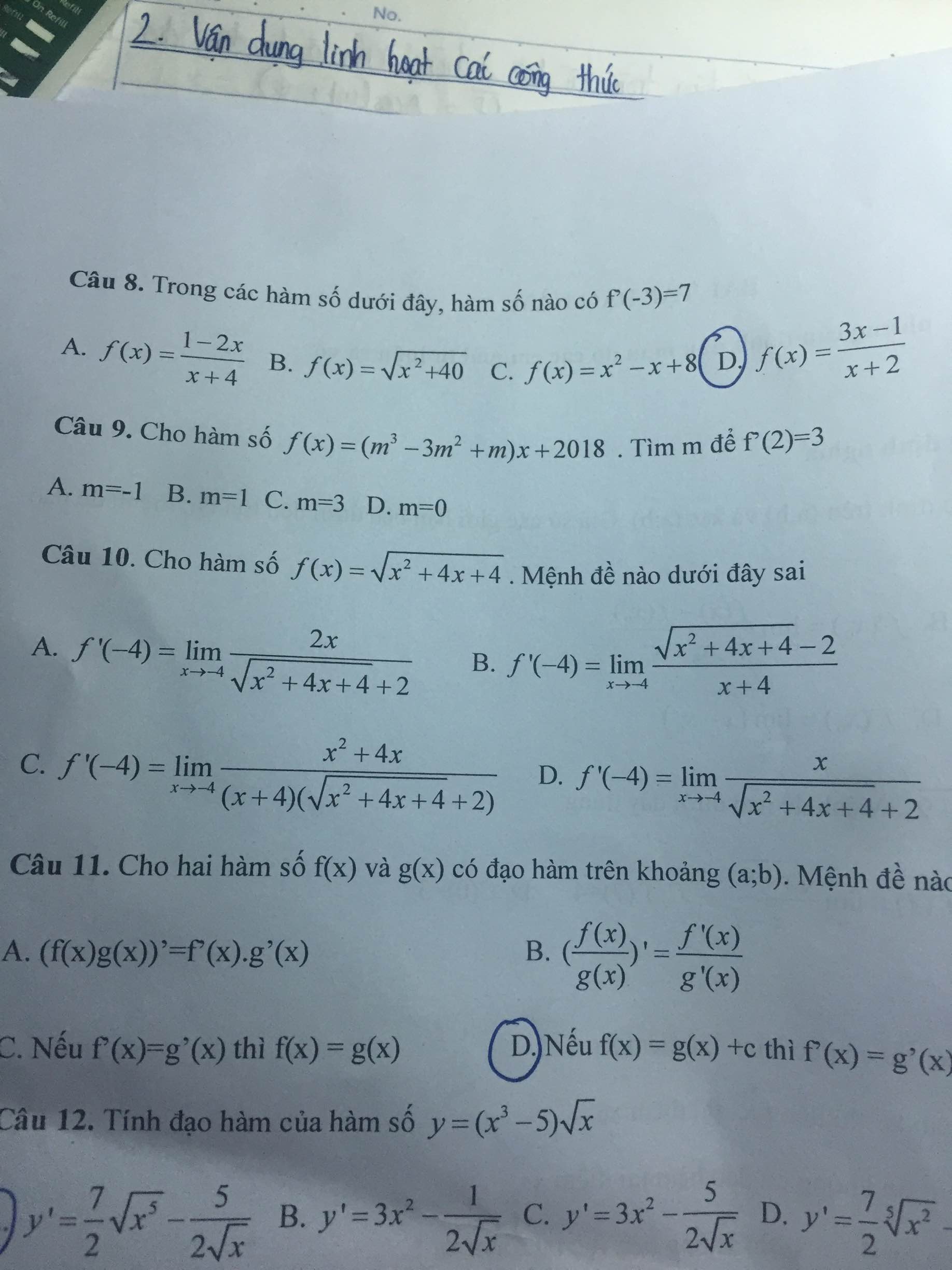



Câu 9)
\(F'(x)=3x^2+2x+1\Rightarrow F(x)=\int (3x^2+2x+1)dx\)
\(\Rightarrow F(x)=x^3+x^2+x+t\) với $t$ là một hằng số nào đó
Vì đồ thị \(y=F(x)\) cắt trục tung tại $c$ nên $c=y=t$
Do đó \(F(x)=x^3+x^2+x+c\)
Phương án D
Câu 10)
Theo đề bài có \(\int f(2x-3)d(2x-3)=F(2x-3)+c\)
\(\Leftrightarrow 2\int f(2x-3)dx=F(2x-3)+c\Rightarrow \int f(2x-3)dx=\frac{F(2x-3)}{2}+c\)
Đáp án C