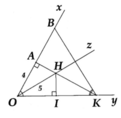
Cho góc xOy nhọn, lấy 2 điểm A và B lần lượt trên cạnh Ox và Oy sao cho OA=OB. Từ A kẻ AH vuông góc với Oy tại H, từ B kẻ BH vuông góc với Ox tại K.
a) CMR: OH=OK b) AH cắt BK tại I. CMR: tia IO là tia phân giác của góc HIK
c) CMR: \(\Delta IHB=\Delta IKA\) c) Gọi C là trung điểm của AB. CMR: O;I;C thẳng hàng.


a: Xét ΔOKB vuông tại K và ΔOHA vuông tại H có
OB=OA
góc BOK chung
Do đó:ΔOKB=ΔOHA
Suy ra: OK=OH
b: Xét ΔOKI vuông tại K và ΔOHI vuông tại H có
OI chung
OK=OH
Do đó:ΔOKI=ΔOHI
Suy ra: \(\widehat{KOI}=\widehat{HOI}\)
hay OI là tia phân giác của góc KOH
c: Xét ΔIHB vuông tại H và ΔIKA vuông tại K có
IH=IK
BH=AK
Do đó:ΔIHB=ΔIKA